题目内容
【题目】给定椭圆C: ![]() +
+ ![]() =1(a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为
=1(a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为 ![]() ,且经过点(0,1).
,且经过点(0,1).
(1)求实数a,b的值;
(2)若过点P(0,m)(m>0)的直线l与椭圆C有且只有一个公共点,且l被椭圆C的伴随圆C1所截得的弦长为2 ![]() ,求实数m的值.
,求实数m的值.
【答案】
(1)解:记椭圆C的半焦距为c.
由题意,得b=1, ![]() =
= ![]() ,c2=a2+b2,
,c2=a2+b2,
解得a=2,b=1.
(2)解:由(1)知,椭圆C的方程为 ![]() +y2=1,圆C1的方程为x2+y2=5.
+y2=1,圆C1的方程为x2+y2=5.
显然直线l的斜率存在.
设直线l的方程为y=kx+m,即kx﹣y+m=0.
因为直线l与椭圆C有且只有一个公共点,
故方程组 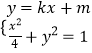 (*)有且只有一组解.
(*)有且只有一组解.
由(*)得(1+4k2)x2+8kmx+4m2﹣4=0.
从而△=(8km)2﹣4(1+4k2)( 4m2﹣4)=0.
化简,得m2=1+4k2.①…(10分)
因为直线l被圆x2+y2=5所截得的弦长为2 ![]() ,
,
所以圆心到直线l的距离d= ![]() =
= ![]() .
.
即 ![]() =
= ![]() . ②
. ②
由①②,解得k2=2,m2=9.
因为m>0,所以m=3.
【解析】(1)记椭圆C的半焦距为c.由题意,得b=1, ![]() =
= ![]() ,由此能求出a,b.(2)由(1)知,椭圆C的方程为
,由此能求出a,b.(2)由(1)知,椭圆C的方程为 ![]() +y2=1,圆C1的方程为x2+y2=5.设直线l的方程为y=kx+m,由
+y2=1,圆C1的方程为x2+y2=5.设直线l的方程为y=kx+m,由 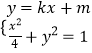 ,得(1+4k2)x2+8kmx+4m2﹣4=0.由此利用根的判别式、弦长公式、圆心到直线的距离,结合知识点能求出m.
,得(1+4k2)x2+8kmx+4m2﹣4=0.由此利用根的判别式、弦长公式、圆心到直线的距离,结合知识点能求出m.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目