题目内容
(1)写出数列
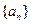 的前3项;
的前3项;(2)求数列
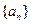 的通项公式(写出推证过程);
的通项公式(写出推证过程);(3)设
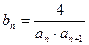 ,
,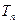 是数列
是数列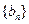 的前
的前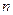 项和,求使得
项和,求使得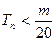 对所有n
对所有n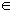 N+都成立的最小正整数
N+都成立的最小正整数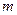 的值。
的值。(1)2,6,10
(2)略
(3)10
解:(1) 当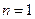 时
时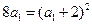 ∴
∴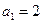
当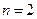 时
时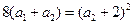 ∴
∴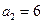
当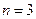 时
时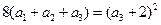 ∴
∴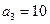 …………3分
…………3分
(2)∵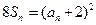 ∴
∴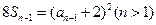
两式相减得: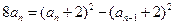 —————————————————5分
—————————————————5分
即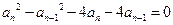
也即
∵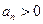 ∴
∴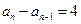 即
即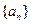 是首项为2,公差为4的等差数列—————7分
是首项为2,公差为4的等差数列—————7分
∴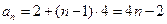 …………8分
…………8分
(3)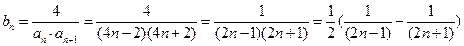 -----10分
-----10分
∴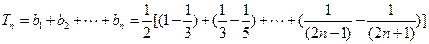
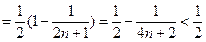 …………12分
…………12分
∵ 对所有
对所有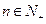 都成立 ∴
都成立 ∴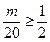 即
即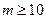
故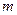 的最小值是10 。 …………14分
的最小值是10 。 …………14分
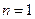 时
时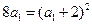 ∴
∴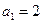
当
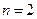 时
时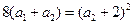 ∴
∴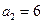
当
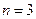 时
时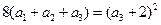 ∴
∴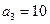 …………3分
…………3分(2)∵
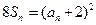 ∴
∴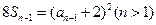
两式相减得:
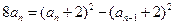 —————————————————5分
—————————————————5分即
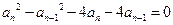
也即

∵
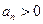 ∴
∴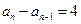 即
即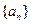 是首项为2,公差为4的等差数列—————7分
是首项为2,公差为4的等差数列—————7分∴
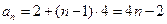 …………8分
…………8分(3)
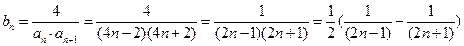 -----10分
-----10分∴
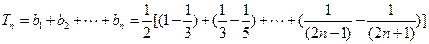
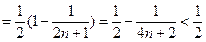 …………12分
…………12分∵
 对所有
对所有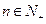 都成立 ∴
都成立 ∴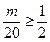 即
即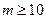
故
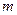 的最小值是10 。 …………14分
的最小值是10 。 …………14分
练习册系列答案
相关题目
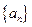 满足
满足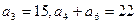 ,
,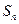 为
为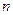 项和.
项和.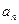 及当
及当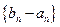 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列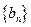 的通项公式及其前
的通项公式及其前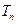 .
.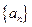 中,
中,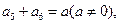
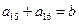 ,则
,则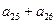 的值是 ( )
的值是 ( )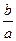
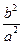
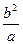
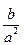
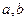 为正实数,
为正实数,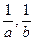 的等差中项为
的等差中项为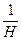 ;
;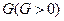 ,则( )
,则( )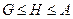 ;
;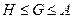 ;
;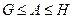 ;
;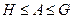 。
。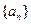 的公差为
的公差为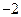 ,且
,且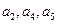 成等比数列,则
成等比数列,则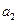 等于( )
等于( )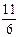
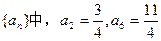
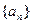 的通项公式;
的通项公式;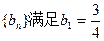 ,且
,且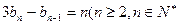 ),求证
),求证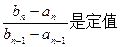 ;
;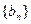 通项公式及前n项和
通项公式及前n项和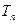 。
。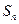 是等差数列
是等差数列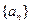 的前
的前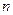 项和,且
项和,且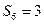 ,
,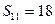 ,则
,则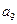 等于( )
等于( )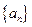 是公比为
是公比为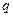 的等比数列,且
的等比数列,且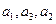 成等差数列,则公比
成等差数列,则公比


