题目内容
已知幂函数 (p∈N)在(0,+∞)上是增函数,且在定义域上是偶函数.
(p∈N)在(0,+∞)上是增函数,且在定义域上是偶函数.
(1)求p的值,并写出相应的f(x)的解析式;
(2)对于(1)中求得的函数f(x),设函数g(x)=-qf[f(x)]+(2q-1)f(x)+1,问:是否存在实数q(q<0),使得g(x)在区间(-∞,-4]上是减函数,且在区间(-4,0)(10)上是增函数?若存在,请求出来;若不存在,请说明理由.
解:(1)因为函数在(0,+∞)上是增函数得:
∴ p2+p+
p2+p+ >0,解得-1<p<3
>0,解得-1<p<3
又因为p∈N
则p=0,2
函数为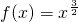 不为偶函数
不为偶函数
则p=1.
故f(x)=x2.
(2)存在.
可设x2=t
则函数g(x)=-qf(x)+(2q-1)x2+1=-qt2+(2q-1)t+1,t≥0,
得其对称轴为t=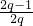 又q<0,所以抛物线开口向上,
又q<0,所以抛物线开口向上,
g(x)在区间(-∞,-4)上是减函数,且在(-4,0)上是增函数
所以t必须在区间(16,+∞)上是减函数,且在(0,16)上是增函数
又t=x2本身是增函数,那么对称轴要等于16
即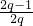 =16 解得q=-
=16 解得q=-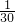
满足(q<0)的条件.
所以存在实数q(q<0),使得g(x)在区间(-∞,-4]上是减函数,且在区间(-4,0)(10)上是增函数.
分析:(1)因为幂函数因为函数在(0,+∞)上是增函数得:得到 p2+p+
p2+p+ >0,求出p的解集,找出整数解即可.又因为函数是偶函数得到p的整数解,最后写出相应的f(x)的解析式;
>0,求出p的解集,找出整数解即可.又因为函数是偶函数得到p的整数解,最后写出相应的f(x)的解析式;
(2)对于存在性问题,可先假设存在,即假设存在实数q(q<0),使得g(x)在区间(-∞,-4]上是减函数,且在区间(-4,0)(10)上是增函数,再利用复合函数的单调性,求出q的值,若出现矛盾,则说明假设不成立,即不存在;否则存在.
点评:考查学生幂函数的性质掌握能力,函数奇偶性的判断能力,以及函数单调性的应用能力.
∴
 p2+p+
p2+p+ >0,解得-1<p<3
>0,解得-1<p<3又因为p∈N
则p=0,2
函数为
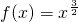 不为偶函数
不为偶函数则p=1.
故f(x)=x2.
(2)存在.
可设x2=t
则函数g(x)=-qf(x)+(2q-1)x2+1=-qt2+(2q-1)t+1,t≥0,
得其对称轴为t=
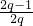 又q<0,所以抛物线开口向上,
又q<0,所以抛物线开口向上,g(x)在区间(-∞,-4)上是减函数,且在(-4,0)上是增函数
所以t必须在区间(16,+∞)上是减函数,且在(0,16)上是增函数
又t=x2本身是增函数,那么对称轴要等于16
即
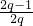 =16 解得q=-
=16 解得q=-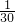
满足(q<0)的条件.
所以存在实数q(q<0),使得g(x)在区间(-∞,-4]上是减函数,且在区间(-4,0)(10)上是增函数.
分析:(1)因为幂函数因为函数在(0,+∞)上是增函数得:得到
 p2+p+
p2+p+ >0,求出p的解集,找出整数解即可.又因为函数是偶函数得到p的整数解,最后写出相应的f(x)的解析式;
>0,求出p的解集,找出整数解即可.又因为函数是偶函数得到p的整数解,最后写出相应的f(x)的解析式;(2)对于存在性问题,可先假设存在,即假设存在实数q(q<0),使得g(x)在区间(-∞,-4]上是减函数,且在区间(-4,0)(10)上是增函数,再利用复合函数的单调性,求出q的值,若出现矛盾,则说明假设不成立,即不存在;否则存在.
点评:考查学生幂函数的性质掌握能力,函数奇偶性的判断能力,以及函数单调性的应用能力.

练习册系列答案
相关题目

 (p∈N)在(0,+∞)上是增函数,且在定义域上是偶函数.
(p∈N)在(0,+∞)上是增函数,且在定义域上是偶函数.