Question

已知点A（－2,0），B（2,0），动点P满足：∠APB=2θ,且|PA||PB|sin²θ=2

（1）证明：动点P的轨迹Q是双曲线；

（2）过点B的直线l与轨迹Q交于两点．试问x轴上是否存在定点C，使为常数，若存在，求出点C的坐标；若不存在，说明理由．

Answer 1

解: （1）依题意，由余弦定理得：

,                           ……2分

即即

　　

．

,即．　　          …………4分

（当动点与两定点共线时也符合上述结论）

动点的轨迹为以为焦点,实轴长为的双曲线．

所以，轨迹Q的方程为．                               …………6分

（2）假设存在定点,使为常数．

（1）当直线 不与轴垂直时，

设直线的方程为,代入整理得:

．                              …………7分

由题意知，．

设,,则,．        …………8分

于是，            …………9分

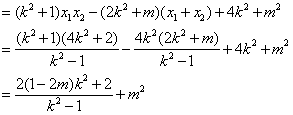
．                      …………11分

要使是与无关的常数，当且仅当，此时．   …12分

（2）当直线 与轴垂直时，可得点,，

当时，．                        …13分

故在轴上存在定点,使为常数．                  …………14分