题目内容
设f(x)=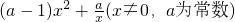 .
.
(Ⅰ)讨论f(x)的奇偶性,并说明理由;
(Ⅱ)当a=2,求f(x)的极值.
解:(Ⅰ)当a=0时,f(x)=-x2为偶函数当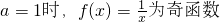
当a≠0且a≠1时,∵f(-1)=-1,f(2)=2a-1.f(-1)+f(1)=2(a-1)≠0
∴f(x)不是奇函数f(-1)-f(1)=-2a≠0∴f(x)不是奇函数
故此时f(x)非奇非偶.
(Ⅱ)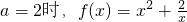
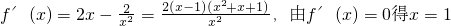
列表如下:
故f(x)= 有极小值3.
有极小值3.
分析:(Ⅰ)讨论a,当a=0,a=1时以及当a≠0且a≠1时根据函数奇偶性的定义进行判定即可;
(Ⅱ当a=2,求出f(x)的导函数f′(x)=0求出方程的解,根据解将区间分成几段,然后判定每一段的导数符号,最后根据极值的判定方法进行判定即可,从而求出极值.
点评:本题主要考查了函数奇偶性的判定,以及导函数计算和极值的判定,同时考查了分类讨论的思想,属于中档题.
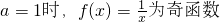
当a≠0且a≠1时,∵f(-1)=-1,f(2)=2a-1.f(-1)+f(1)=2(a-1)≠0
∴f(x)不是奇函数f(-1)-f(1)=-2a≠0∴f(x)不是奇函数
故此时f(x)非奇非偶.
(Ⅱ)
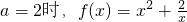
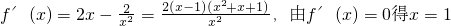
列表如下:
| x | (-∞,0) | (0,1) | 1 | (1,+∞) |
| f′(x) | - | - | 0 | + |
| f(x) | ↘ | ↘ | 极小值 f(1)=3 | ↗ |
 有极小值3.
有极小值3.分析:(Ⅰ)讨论a,当a=0,a=1时以及当a≠0且a≠1时根据函数奇偶性的定义进行判定即可;
(Ⅱ当a=2,求出f(x)的导函数f′(x)=0求出方程的解,根据解将区间分成几段,然后判定每一段的导数符号,最后根据极值的判定方法进行判定即可,从而求出极值.
点评:本题主要考查了函数奇偶性的判定,以及导函数计算和极值的判定,同时考查了分类讨论的思想,属于中档题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
设f(x)在[0,1]上有定义,要使函数f(x-a)+f(x+a)有定义,则a的取值范围为( )
A、(-∞,-
| ||||
B、[-
| ||||
C、(
| ||||
D、(-∞,-
|