题目内容
设数列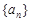 是公差为
是公差为 的等差数列,其前
的等差数列,其前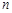 项和为
项和为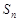 ,已知
,已知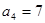 ,
,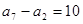 。
。
(1)求数列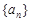 的通项
的通项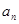 及前
及前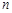 项和为
项和为 ;
;
(2)求证: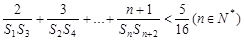 。
。
(1) (2)对于证明不等式的成立,关键是对于左边和式的求解,然后借助于函数的思想来证明。
(2)对于证明不等式的成立,关键是对于左边和式的求解,然后借助于函数的思想来证明。
解析试题分析:解:(1)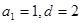 2分
2分
所以 2分
2分
(2)因为 3分
3分
所以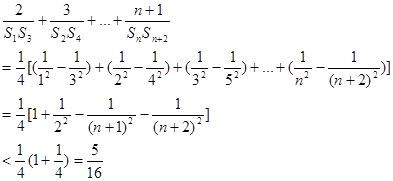 3分
3分
考点:等差数列,裂项求和
点评:主要是考查了数列的通项公式和数列求和的综合运用,属于常规题,计算要细心。

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 是函数
是函数 且
且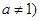 的图像上一点,等比数列
的图像上一点,等比数列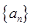 的前
的前 项的和为
项的和为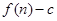 ;数列
;数列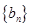
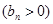 的首项为
的首项为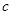 ,且前
,且前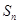 满足
满足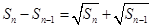
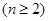 .
.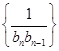 的前
的前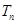 ,问
,问 的最小正整数
的最小正整数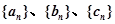 满足
满足
 ,当
,当 时,求数列
时,求数列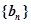 的通项公式.
的通项公式.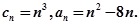 求正整数
求正整数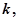 使得一切
使得一切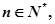 均有
均有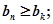
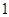
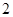
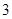
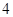
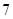
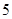
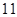
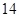
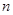 行的第二个数为
行的第二个数为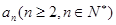 .
.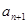 的关系式,并求出
的关系式,并求出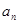 的通项公式.
的通项公式.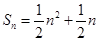
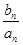 ,求数列
,求数列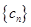 的通项公式
的通项公式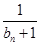 +
+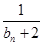 +…+
+…+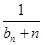 >
>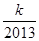 对任意正整数n均成立?若存在,求出k的最大值,若不存在,说明理由.
对任意正整数n均成立?若存在,求出k的最大值,若不存在,说明理由.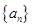 中,
中,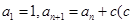 为常数,
为常数, ,且
,且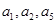 成公比不等于1的等比数列.
成公比不等于1的等比数列.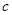 的值;
的值; ,求数列
,求数列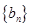 的前
的前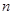 项和
项和 。
。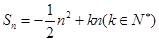 ,且Sn的最大值为8.
,且Sn的最大值为8.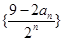 的前n项和Tn。
的前n项和Tn。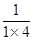 ,
,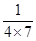 ,
,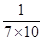 ,……,
,……, ,……
,……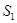 ,
,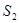 ,
,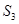 ,
,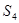
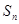 的表达式并用数学归纳法证明你的猜想。
的表达式并用数学归纳法证明你的猜想。