题目内容
解答题:应写出文字说明、证明过程或演算步骤
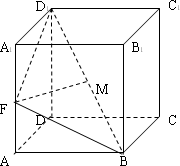
如下图所示:四面体ABCD中,AB、BC、BD两两互相垂直,且AB=BC=2,E是AC中点,异面直线AD与BE所成角的余弦值为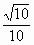 .
.
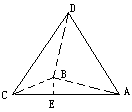
(1)求二面角D—AC—B的大小;
(2)求二面角D—AC—B的正切值;
(3)求点B到平面ACD的距离.
答案:
解析:
解析:
|
(1)(2)取CD的中点F,连结BF、EF,设BD=x.则EF=
∴EF=FB 即△BEF为等腰三角形 ∵BE= 由 得 解得 ∴x=4 连结DE,∵DE⊥AC,BE⊥AC, ∴∠BED是二面角D—AC—B的平面角 tan∠BED= 即二面角D—AC—B的正切值为 (3)过B作BH⊥DE于H,∵平面BDE⊥平面ACD,
∴BH⊥平面ACD,即BH为所求 ∵BH·DE=BD·BE,∴BH= ∴点B到平面ACD的距离为 |

练习册系列答案
相关题目
| |||||||||||||||
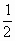 AD
AD
 ,cos∠BEF=
,cos∠BEF=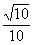
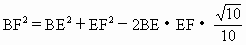
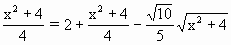
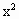 =16
=16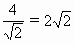
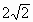 (二面角D—AC—B的大小arctan
(二面角D—AC—B的大小arctan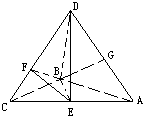
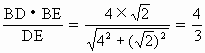
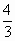
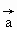 |=1,|
|=1,|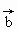 |=2,
|=2,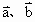 ;
;

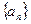 中,
中,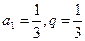 ,
,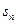 为数列
为数列 项的和,证明:
项的和,证明:
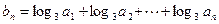 ,求数列
,求数列 的通项公式;
的通项公式;