��Ŀ����
5��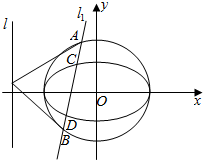 ��֪ԲC1��x2+y2=r2����Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����x��Ľ����غϣ�����ԲC2��������Ϊ$\frac{\sqrt{2}}{2}$��ԲC1�ϵĵ㵽ֱ��l��x=-2$\sqrt{2}$����̾���Ϊ2$\sqrt{2}$-2��
��֪ԲC1��x2+y2=r2����Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����x��Ľ����غϣ�����ԲC2��������Ϊ$\frac{\sqrt{2}}{2}$��ԲC1�ϵĵ㵽ֱ��l��x=-2$\sqrt{2}$����̾���Ϊ2$\sqrt{2}$-2����1������ԲC2�ķ��̣�
��2����ͼ��ֱ��1�ϵĶ���T��ԲC1���������ߣ����е�ֱ�ΪA��B����ֱ��AB����ԲC2���ڲ�ͬ������C��D�����OCD��������ֵ��
���� ��1�����������ʹ�ʽ��ֱ�ߺ�Բ��λ�ù�ϵ���Լ�a��b��c�Ĺ�ϵ���ⷽ�̿ɵ�a��b�������õ���Բ���̣�
��2��ԲC1�ķ���Ϊx2+y2=4����ֱ��x=-2$\sqrt{2}$�ϵĶ���T������Ϊ��-2$\sqrt{2}$��t������t��R������A��x1��y1����B��x2��y2������ֱ��AT�ķ���Ϊx1x+y1y=4��ֱ��BT�ķ���Ϊx2x+y2y=4��ֱ��AB�ķ���Ϊ-2$\sqrt{2}$x+ty=2���ɴ����õ㵽ֱ�ߵľ��빫ʽ�ɵ�O��ֱ��AB�ľ��룬����ֱ�߷��̺���Բ��������������Τ�ﶨ�����ҳ���ʽ�����������ε������ʽ�������������ɻ�������ʽ���ɵõ����ֵ��
��� �⣺��1��������ɵ�e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$��r=a��
��2$\sqrt{2}$-a=2$\sqrt{2}$-2��a2-b2=c2��
���a=2��b=c=$\sqrt{2}$��
������Բ����Ϊ$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1��
��2��ԲC1�ķ���Ϊx2+y2=4��
��ֱ��x=-2$\sqrt{2}$�ϵĶ���T������Ϊ��-2$\sqrt{2}$��t������t��R����
��A��x1��y1����B��x2��y2������ֱ��AT�ķ���Ϊx1x+y1y=4��
ֱ��BT�ķ���Ϊx2x+y2y=4��
��T��-2$\sqrt{2}$��t����ֱ��AT��BT�ϣ��� $\left\{\begin{array}{l}{-2\sqrt{2}{x}_{1}+t{y}_{1}=4}\\{-2\sqrt{2}{x}_{2}+t{y}_{2}=4}\end{array}\right.$��
��ֱ��AB�ķ���Ϊ-2$\sqrt{2}$x+ty=4��
��ԭ��O��ֱ��AB�ľ���Ϊd=$\frac{4}{\sqrt{8+{t}^{2}}}$��
����$\left\{\begin{array}{l}{-2\sqrt{2}x+ty=4}\\{{x}^{2}+2{y}^{2}=4}\end{array}\right.$����ȥx���ã�t2+16��y2-8ty-16=0��
��C��x3��y3����D��x4��y4����
��y3+y4=$\frac{8t}{{t}^{2}+16}$��y3y4=-$\frac{16}{{t}^{2}+16}$��
�Ӷ�|CD|=$\sqrt{1+\frac{{t}^{2}}{8}}$|y3-y4|=$\frac{1}{4}$$\sqrt{16+2{t}^{2}}$•$\sqrt{��\frac{8t}{16+{t}^{2}}��^{2}+\frac{64}{{t}^{2}+16}}$=$\frac{4��8+{t}^{2}��}{16+{t}^{2}}$��
���OCD���ΪS=$\frac{1}{2}$d•|CD|=$\frac{1}{2}$•$\frac{4}{\sqrt{8+{t}^{2}}}$•$\frac{4��8+{t}^{2}��}{16+{t}^{2}}$=$\frac{8\sqrt{8+{t}^{2}}}{16+{t}^{2}}$��
��$\sqrt{8+{t}^{2}}$=m��m��2$\sqrt{2}$��������S=$\frac{8m}{8+{m}^{2}}$=$\frac{8}{m+\frac{8}{m}}$��$\frac{8}{2\sqrt{m•\frac{8}{m}}}$=$\sqrt{2}$��
���ҽ���m=$\frac{8}{m}$���ɵ�m=2$\sqrt{2}$����OCD�����ȡ�����ֵ$\sqrt{2}$��
���� ���⿼����Բ�ķ��̵���ע��������Բ�����ʺ�ֱ�ߺ�Բ��λ�ù�ϵ�����������ε���������ֵ����ע����������ֱ�߷��̺���Բ���̣�����Τ�ﶨ�����ҳ���ʽ���Լ���������ʽ�����ֵ�������е��⣮

| A�� | {y|y��1} | B�� | {y|y��1} | C�� | {y|y��0} | D�� | {y|y��0} |
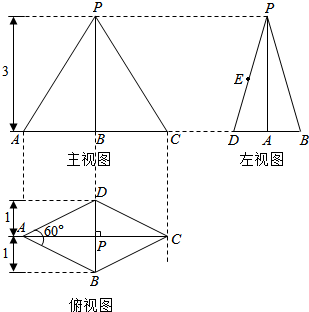 һ������������ͼ��ֱ��ͼ��ͼ��ʾ��EΪ����PD���е㣮
һ������������ͼ��ֱ��ͼ��ͼ��ʾ��EΪ����PD���е㣮