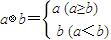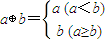题目内容
 对a,b∈R,定义:min{a,b}=
对a,b∈R,定义:min{a,b}=
|
(1)求f(-2),f(3)的值;
(2)在平面直角坐标系内作出该函数的大致图象;
(3)就k的值讨论关于x的方程f(x)=k解的个数情况.
分析:(1)根据已知条件中的新定义直接求出f(-2),f(3)的值;
(2)先利用题中的新定义将函数f(x)写成分段函数的形式,再分段画出其图象即可;
(3)对k进行分类讨论,分别讨论方程实根的个数,最后结合(2)中的图象得出结论即可.
(2)先利用题中的新定义将函数f(x)写成分段函数的形式,再分段画出其图象即可;
(3)对k进行分类讨论,分别讨论方程实根的个数,最后结合(2)中的图象得出结论即可.
解答: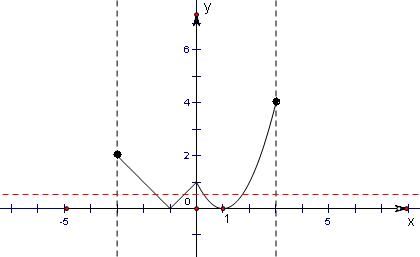 解:(1)f(-2)=min{(-2-1)2,|-2+1|}=1,
解:(1)f(-2)=min{(-2-1)2,|-2+1|}=1,
f(3)=min{(3-1)2,|3+1|}=4.
(2)f(x)=
.
在平面直角坐标系内作出该函数的大致图象,如图所示.
(3)由f(x)的图象可知,
当k=0时,方程f(x)=k解的个数是2;
当0<k<1时,方程f(x)=k解的个数是4;
当k=1时,方程f(x)=k解的个数是3;
当1<k≤2时,方程f(x)=k解的个数是2;
当2<k<4时,方程f(x)=k解的个数是1.
 解:(1)f(-2)=min{(-2-1)2,|-2+1|}=1,
解:(1)f(-2)=min{(-2-1)2,|-2+1|}=1,f(3)=min{(3-1)2,|3+1|}=4.
(2)f(x)=
|
在平面直角坐标系内作出该函数的大致图象,如图所示.
(3)由f(x)的图象可知,
当k=0时,方程f(x)=k解的个数是2;
当0<k<1时,方程f(x)=k解的个数是4;
当k=1时,方程f(x)=k解的个数是3;
当1<k≤2时,方程f(x)=k解的个数是2;
当2<k<4时,方程f(x)=k解的个数是1.
点评:本题主要考查了分段函数的解析式求法及其图象的作法,考查了方程的根的个数判断.解答的关键 是利用函数与方程及数形结合的思想方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目