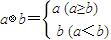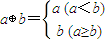Question

对?a，b∈R，定义：max{a，b}=

a，(a≥b) b，(a＜b)

，min{a，b}=

a，(a＜b) b，(a≥b)

．则下列各式：
（1）max{a，b}=

1

2

（a+b-|a-b|）
（2）max{a，b}=

1

2

（a+b+|a-b|）
（3）min{a，b}=

1

2

（a+b+|a-b|）
（4）min{a，b}=

1

2

（a+b-|a-b|）
其中恒成立的是（　　）

A．（1）（2）（3）（4）

B．（1）（2）（3）

C．（1）（3）

D．（2）（4）

Answer 1

分析：根据绝对值的代数意义，非负数的绝对值等于其本身，非正数的绝对值等于他的相反数，将绝对值符号去掉化为分段函数的形式，可得答案．

解答：解：∵

1

2

（a+b+|a-b|）=

1 2 (a+b+a-b)，(a≥b) 1 2 (a+b-a+b)，(a＜b)

=

a，(a≥b) b，(a＜b)

=max{a，b}；

1

2

（a+b-|a-b|）=

1 2 (a+b+a-b)，(a＜b) 1 2 (a+b-a+b)，(a≥b)

=

a，(a＜b) b，(a≥b)

=min{a，b}
故选D

点评：本题考查的知识点是绝对值函数，根据绝对值的代数意义，将原式中绝对值符号去掉化为分段函数的形式，是解答的关键．