题目内容
对?a、b∈R,定义运算“?”、“⊕”为: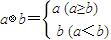
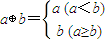
给出下列各式
①(sinx?cosx)+(sinx⊕cosx)=sinx+cosx,②(2x?x2)-(2x⊕x2)=2x-x2,
③(sinx?cosx)•(sinx⊕cosx)=sinx•cosx,④(2x?x2)÷(2x⊕x2)=2x÷x2.
其中等式恒成立的是 .(将所有恒成立的等式的序号都填上)
【答案】分析:利用新定义的函数概念化简所给式子的左边得出:①当sinx≥cosx时,当sinx<cosx时,证得①成立;同理③也成立;②取特殊值:当x=2时,证得:2x?x2)-(2x⊕x2)=2x-x2≠2x-x2,故错;同理④错.
解答:解:①当sinx≥cosx时,sinx?cosx=sinx,sinx⊕cosx=cosx,故(sinx?cosx)+(sinx⊕cosx)=sinx+cosx,
当sinx<cosx时,sinx?cosx=cosx,sinx⊕cosx=sinx,故(sinx?cosx)+(sinx⊕cosx)=sinx+cosx,故正确;
同理③也成立;
②当x=2时,2x?x2=x2,2x⊕x2=2x
∴(2x?x2)-(2x⊕x2)=x2-2x≠2x-x2,故错;
同理④错.
故答案为:①③.
点评:当遇到函数创新应用题型时,处理的步骤一般为:化简解析式,求函数解析式的最简形式.
解答:解:①当sinx≥cosx时,sinx?cosx=sinx,sinx⊕cosx=cosx,故(sinx?cosx)+(sinx⊕cosx)=sinx+cosx,
当sinx<cosx时,sinx?cosx=cosx,sinx⊕cosx=sinx,故(sinx?cosx)+(sinx⊕cosx)=sinx+cosx,故正确;
同理③也成立;
②当x=2时,2x?x2=x2,2x⊕x2=2x
∴(2x?x2)-(2x⊕x2)=x2-2x≠2x-x2,故错;
同理④错.
故答案为:①③.
点评:当遇到函数创新应用题型时,处理的步骤一般为:化简解析式,求函数解析式的最简形式.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 对a,b∈R,定义:min
对a,b∈R,定义:min
