题目内容
1．有一个三棱锥与一个四棱锥，棱长都相等，它们的一个侧面重叠后，还有暴露面的个数为（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
分析 画出几何体，由三棱锥和四棱锥的棱长都相等推知三棱锥的各个面和四棱锥的侧面都是正三角形，再分别证得侧棱平行，由面与面平行的判断定理证得两个面平行，由斜三棱柱的结构特征即可得出结论．
解答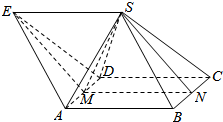 
解：这个组合体为一斜三棱柱，如图所示；
三棱锥为S-AED，正四棱锥为S-ABCD，重合的面为△ASD，
设AD，BC中点分别为M、N，
由题意知AD⊥ME，AD⊥MS，AD⊥MN；
又ME∩MS=M，MN∩MS=M，
∴AD⊥面MNS，由AD⊥面MES，且面MNS∩面MES=MS，
∴面MNS与面MES重合；
又∵SE=AB=MN，EM=SN，
∴MNSE为平行四边行，
又MN∥AB，∴AB∥SE；
∴四边形ABSE为平行四边形，四边形CDES为平行四边形，
∴SC∥DE，SB∥AE；
又SC∩SB=S，AE∩DE=E，
∴面SBC∥面EAD；
又AB=SE=CD，AB不垂直于面SBC，
∴组合体为斜三棱柱，暴露面的个数为5．
故选：B．
点评 本题考查了空间几何体的结构特征，也考查了空间形象能力与逻辑推理能力，是综合性题目．
练习册系列答案
阅读快车系列答案
相关题目
11．在棱长为1的正方体ABCD-A1B1C1D1中，B1点到平面ACD1的距离为（ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{2\sqrt{3}}{3}$ | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
9．已知$f（x）=\left\{\begin{array}{l}{|lg|x||\\;x≠0}\\{0\\;x=0}\end{array}\right.$，关于x的方程f2（x）+bf（x）+c=0有7个不同的解，则满足b，c的条件是（ ）
| A． | b＜0，c＜0 | B． | b＜0，c=0 | C． | b＞0，c=0 | D． | b＞0，c＜0 |
6．高为1的四棱锥S-ABCD的底面是边长为2的正方形，点S、A、B、C、D均在半径为$\frac{\sqrt{17}}{2}$的同一球面上，在底面ABCD的中心与顶点S之间的距离为（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{5}}{2}$ | C． | $\sqrt{5}$ | D． | $\sqrt{2}$ |
13．
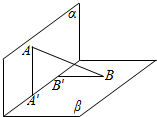如图，平面α⊥平面β，A∈α，B∈β，AB与两平面α，β所成的角分别为$\frac{π}{4}$和$\frac{π}{6}$，线段AB在α∩β=l上的射影为 A′B′，若AB=12，则A′B′=（ ）
如图，平面α⊥平面β，A∈α，B∈β，AB与两平面α，β所成的角分别为$\frac{π}{4}$和$\frac{π}{6}$，线段AB在α∩β=l上的射影为 A′B′，若AB=12，则A′B′=（ ）| A． | 4 | B． | 6 | C． | 8 | D． | 9 |
10．已知α∩β=l，a?α，b?β，且a，b是异面直线，那么直线l（ ）
| A． | 至多与a，b中的一条相交 | B． | 至少与a，b中的一条平行 | ||
| C． | 与a，b都相交 | D． | 至少与a，b中的一条相交 |