题目内容
正三棱锥S—ABC的侧棱与底面边长相等,如果E、F分别为SC、AB的中点,那么异面直线EF与SA所成的角等于( )A.90° B.60° C.45° D.30°
答案:C
解析:如图,取SB、BC中点分别为G、H,连结GF、GE、SH、AH,设正三棱锥的棱长为1,则GF∥SA且GF=![]() SA=
SA=![]() ,GE∥BC,GE=
,GE∥BC,GE=![]() BC=
BC=![]() .
.

∴EF与SA所成的角为∠GFE.
又BC⊥平面SAH,
∴BC⊥SA.∴GE⊥GF.
在△GEF中,GE=GF=![]() ,∠FGE=90°,∴∠GFE=45°.故选C.
,∠FGE=90°,∴∠GFE=45°.故选C.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
已知正三棱锥S-ABC的三条侧棱两两互相垂直,且SA=2
,则正三棱锥S-ABC的外接球的表面积是( )
| 3 |
| A、12π | B、32π |
| C、36π | D、48π |
 如图,正三棱锥S-ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.
如图,正三棱锥S-ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.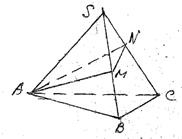 正三棱锥S-ABC的侧棱长为2,侧面等腰三角形的顶角为30°,过底面顶点作截面△AMN交侧棱SB、SC分别于M、N两点,则△AMN周长的最小值是
正三棱锥S-ABC的侧棱长为2,侧面等腰三角形的顶角为30°,过底面顶点作截面△AMN交侧棱SB、SC分别于M、N两点,则△AMN周长的最小值是
 如图正三棱锥S-ABC的侧棱与底面边长相等,如果E、F分别是SC、AB的中点,那么异面直线EF与SA所成的角为
如图正三棱锥S-ABC的侧棱与底面边长相等,如果E、F分别是SC、AB的中点,那么异面直线EF与SA所成的角为