题目内容

17．函数y=2x+$\sqrt{2x-1}$的值域为[1，+∞）．

分析 由题意知2x-1≥0，从而得2x+$\sqrt{2x-1}$≥1．

解答 解：由题意，2x-1≥0，
故2x+$\sqrt{2x-1}$≥1；
即函数y=2x+$\sqrt{2x-1}$的值域为[1，+∞）；
故答案为：[1，+∞）．

点评 本题考查了函数的值域的求法，属于基础题．

练习册系列答案
相关题目
12．已知函数$f（x）=\sqrt{3}sinx-acosx$（x∈R）的图象经过点$（{\frac{2π}{3}，1}）$．
（1）求函数f（x）的解析式；
（2）设α，$β∈[{0，\frac{π}{2}}]$，$f（{α-\frac{π}{6}}）=\frac{6}{5}$，$f（{β+\frac{5π}{6}}）=-\frac{10}{13}$，求cos（α-β）的值．
8．已知函数f（x）满足f（x）=f′（1）ex-1-f（0）x+$\frac{1}{2}$x2．
（1）求f（x）的解析式；
（2）若g（x）=$\frac{1}{2}$x2+ax+b，解关于x的不等式f′（x）-g′（x）＞0．
5．圆ρ=2sin（θ+$\frac{π}{3}$）的半径和圆心的极坐标分别为1，（1，$\frac{π}{6}$）．
12．已知圆C的方程为x2+y2-4y=0，直线l的方程为y=kx+1．
（1）求圆心的坐标和圆的半径；
（2）求直线l被圆所截得的弦长最短时k的值．
2．如图所示是一个循环结构的算法，下列说法不正确的是（　　）
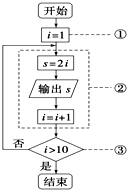
A．①是循环变量初始化，循环就要开始
B．②为循环体
C．③是判断是否继续循环的终止条件
D．输出的S值为2，4，6，8，10，12，14，16，18
9．已知函数f（x）=xex，g（x）=x2-x-a，a∈R．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）若f（x）+g（x）≥0对任意x∈R恒成立，求a的取值范围．
6．已知$\frac{m}{1+i}$=1-ni，其中m，n∈R，i为虚数单位，则m+ni=（　　）
A．2+iB．1+2iC．2-iD．1-2i
7．已知函数f（x）=sin（ωx+φ）（其中ω＞0，|φ|＜$\frac{π}{2}$）图象相邻对称轴的距离为$\frac{π}{2}$，一个对称轴中心为（-$\frac{π}{6}$，0），为了得到g（x）=cosx的图象，则只要将f（x）的图象（　　）
A．向右平移$\frac{π}{6}$个单位B．向右平移$\frac{π}{12}$个单位
C．向左平移$\frac{π}{6}$个单位D．向左平移$\frac{π}{12}$个单位

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网