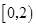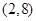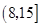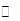题目内容
(本小题满分12分)某商店商品每件成本10元,若售价为25元,则每天能卖出288件,经调查,如果降低价格,销售量可以增加,且每天多卖出的商品件数t与商品单价的降低值 (单位:元,
(单位:元, )的关系是t=
)的关系是t= .
.
(1)将每天的商品销售利润y表示成 的函数;
的函数;
(2)如何定价才能使每天的商品销售利润最大?
【答案】
(1)
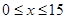 ;(2)17.
;(2)17.
【解析】
试题分析:(1)因为每天的商品销售利润y等于每件的利润乘以每天生产的件数.因为降低价格,销售量可以增加,且每天多卖出的商品件数t.而t与商品单价的降低值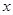 (单位:元,
(单位:元,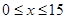 )的关系是t=
)的关系是t= .所以可得每天的利润
.所以可得每天的利润 与单价降低值
与单价降低值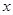 的关系式.
的关系式.
(2)由(1)求得的函数关系式,通过求导求出函数的极值点,以及极大值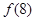 .在对比临界点的值
.在对比临界点的值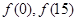 从而可得函数的最大值以及对应的
从而可得函数的最大值以及对应的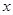 的值.
的值.
试题解析:(1)设商品降价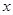 元,记商品每天的获利为
元,记商品每天的获利为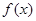 ,则依题意得
,则依题意得
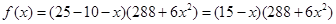
 (
(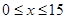 ) -6分
) -6分
(2)根据(1),有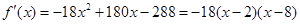 .
.
当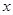 变化时,
变化时,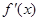 与
与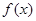 的变化如下表:
的变化如下表:
|
|
|
2 |
|
8 |
|
|
|
|
0 |
|
0 |
|
|
|
|
极小 |
|
极大 |
|
故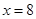 时,
时,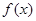 取得极大值.因为
取得极大值.因为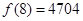 ,
, ,
,
所以定价为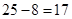 元能使一天的商品销售利润最大. 12分
元能使一天的商品销售利润最大. 12分
考点:1.函数的实际应用.2.函数的最值问题.3.函数的导数.

练习册系列答案
相关题目