题目内容
在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点.已知|AB|=2|OA|,且点B的纵坐标大于零.
(Ⅰ)求向量 的坐标;
的坐标;
(Ⅱ)求圆x2-6x+y2+2y=0关于直线OB对称的圆的方程;
(Ⅲ)是否存在实数a,使抛物线y=ax2-1上总有关于直线OB对称的两个点?若不存在,说明理由;若存在,求a的取值范围.
答案:
解析:
解析:
|
解(Ⅰ)设 所以 v-3>0,得v=8,故 (Ⅱ)由 由条件可知圆的标准方程为:(x-3)2+(y+1)2=10, 得圆心(3,-1),半径为 设圆心(3,-1)关于直线OB的对称点为(x,y),则 故所求圆的方程为(x-1)2+(y-3)2=10. (Ⅲ)设P(x1,y1),Q(x2,y2)为抛物线上关于直线OB对称的两点,则 即x1、x2为方程x2+ 于是由Δ= 故当a> |

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
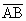 ={u,v},则由
={u,v},则由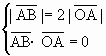 ,即
,即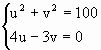 ,得
,得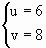 ,或
,或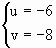 .因为
.因为 =
=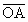 +
+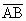 ={u+4,v-3},
={u+4,v-3},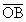 ={10,5},得B(10,5),于是直线OB方程:y=
={10,5},得B(10,5),于是直线OB方程:y=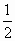 x.
x.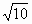 .
.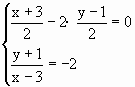 ,得
,得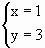 ,
,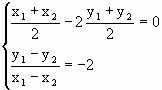 ,得
,得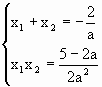 ,
,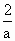 x+
x+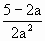 =0的两个相异实根,
=0的两个相异实根,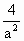 -4·
-4·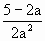 >0,得a>
>0,得a>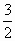 .
.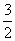 时,抛物线y=ax2-1上总有关于直线OB对称的两点.
时,抛物线y=ax2-1上总有关于直线OB对称的两点. 选考题
选考题 (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. ,求线段AC的长度.
,求线段AC的长度. 的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.
的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程. (α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
(α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.