题目内容
已知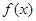 是R上的偶函数,若
是R上的偶函数,若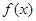 的图象向右平移一个单位后,则得到一
的图象向右平移一个单位后,则得到一
个奇函数的图象,w则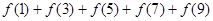 的值为( )
的值为( )
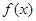 是R上的偶函数,若
是R上的偶函数,若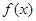 的图象向右平移一个单位后,则得到一
的图象向右平移一个单位后,则得到一个奇函数的图象,w则
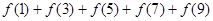 的值为( )
的值为( ) | A.1 | B.0 | C.-1 | D.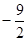 |
B
分析:由题意知,f(x)是R上的偶函数,f(x-1)是一个奇函数,由奇函数的定义得f(x-1)+f(x+1)=0,再由f(1)=f(-1)=0,f(1)+f(3)+…+f(9)=f(1)=0.
解答:解:由题意知,f(x)是R上的偶函数,f(x-1)是一个奇函数,
∴f(x-1)=-f(-x-1)=-f(x+1),
∴f(x-1)+f(x+1)=0,
∴f(9)+f(7)=0,f(5)+f(3)=0,
由f(x-1)是奇函数 得,f(0-1)=0,即f(-1)=0,
又f(x)是R上的偶函数,
∴f(1)=f(-1)=0,
∴f(1)+f(3)+…+f(9)=f(1)=0,
故选 B.
解答:解:由题意知,f(x)是R上的偶函数,f(x-1)是一个奇函数,
∴f(x-1)=-f(-x-1)=-f(x+1),
∴f(x-1)+f(x+1)=0,
∴f(9)+f(7)=0,f(5)+f(3)=0,
由f(x-1)是奇函数 得,f(0-1)=0,即f(-1)=0,
又f(x)是R上的偶函数,
∴f(1)=f(-1)=0,
∴f(1)+f(3)+…+f(9)=f(1)=0,
故选 B.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
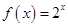 与
与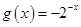 的图象关于( ▲ )
的图象关于( ▲ )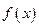 在定义域
在定义域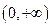 上为增函数,且满足
上为增函数,且满足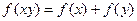 ,
, 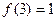 .
.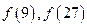 的值;
的值; 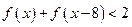 .
.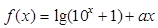 是偶函数,
是偶函数,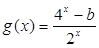 是奇函数,那么
是奇函数,那么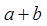 的值为( )
的值为( )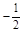
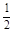
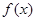 是周期为2的奇函数,当0≤x≤1时,
是周期为2的奇函数,当0≤x≤1时,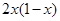 ,则
,则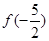 =( )
=( ) 


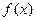 是定义在实数有R上的奇函数,若x≥0时,
是定义在实数有R上的奇函数,若x≥0时,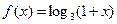 ,则
,则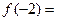 ___ __.
___ __.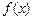 =
=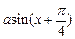 +
+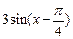 是偶函数,则实数a= .
是偶函数,则实数a= .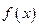 是奇函数,当
是奇函数,当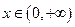 时,
时,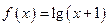 ,则当
,则当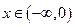 时,
时,