题目内容
设函数![]() ,曲线y=f(x)在点(2,f(2))处的切线方程为y=3.
,曲线y=f(x)在点(2,f(2))处的切线方程为y=3.
(Ⅰ)求y=f(x)的解析式:
(Ⅱ)证明:函数y=f(x)的图像是一个中心对称图形,并求其对称中心;
(Ⅲ)证明:曲线y=f(x)上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值,并求出此定值.
答案:
解析:
提示:
解析:
|
(Ⅰ) 解得 因 (Ⅱ)证明:已知函数 所以函数 而函数 可知,函数 (Ⅲ)证明:在曲线上任一点 由 令 令 直线 从而所围三角形的面积为 所以,所围三角形的面积为定值2. |
提示:
|
导数与函数的结合一直是高考的热点,要重点关注 本题是函数与导数的综合题,主要考查导数的应用,以及函数的有关性质,以及函数与方程的思想,以及分析问题与解决问题的能力. |

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
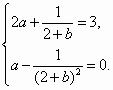
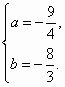
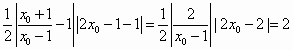 .
.