题目内容
设函数![]() ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
(Ⅰ)求y=f(x)的解析式;
(Ⅱ)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
答案:
解析:
提示:
解析:
|
试题解析: (Ⅰ)方程 又 (Ⅱ)设 令 令 所以点 故曲线 高考考点:导数及直线方程的相关知识 |
提示:
|
运算能力一直是高考考查的能力之一,近年来,对运算能力的要求降低了,但对准确率的要求提高了. |

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
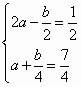 ,解得
,解得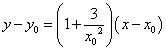 ,即
,即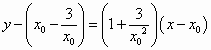
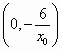 ;
;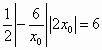 ;
;