题目内容
设曲线y=sin x上任一点(x,y)处切线斜率为g(x),则函数y=x2g(x)的部分图象可以为( ).

C
【解析】y′=cos x,即g(x)=cos x,所以y=x2g(x)=x2cos x为偶函数,图象关于y轴对称,所以排除A,B.由y=x2cos x=0,得x=0或x=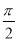 +kπ,k∈Z,即函数图象过原点,所以选C.
+kπ,k∈Z,即函数图象过原点,所以选C.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
题目内容
设曲线y=sin x上任一点(x,y)处切线斜率为g(x),则函数y=x2g(x)的部分图象可以为( ).

C
【解析】y′=cos x,即g(x)=cos x,所以y=x2g(x)=x2cos x为偶函数,图象关于y轴对称,所以排除A,B.由y=x2cos x=0,得x=0或x=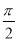 +kπ,k∈Z,即函数图象过原点,所以选C.
+kπ,k∈Z,即函数图象过原点,所以选C.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案