题目内容
在 中,角
中,角 、
、 、
、 所对应的边为
所对应的边为 、
、 、
、 .
.
(1)若 ,求
,求 的值;
的值;
(2)若 ,且
,且 的面积
的面积 ,求
,求 的值.
的值.
(1)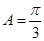 ;(2)
;(2) .
.
解析试题分析:(1)在等式 中利用差角公式化简求出
中利用差角公式化简求出 的值,从而求出角
的值,从而求出角 的值;(2)解法1是先求出
的值;(2)解法1是先求出 的值,借助三角形的面积公式得出
的值,借助三角形的面积公式得出 与
与 之间的等量关系,再利用余弦定理最终得到
之间的等量关系,再利用余弦定理最终得到 与
与 的等量关系,最后利用正弦定理求出
的等量关系,最后利用正弦定理求出 的值;解法2是是先求出
的值;解法2是是先求出 的值,借助三角形的面积公式得出
的值,借助三角形的面积公式得出 与
与 之间的等量关系,再利用余弦定理最终得到
之间的等量关系,再利用余弦定理最终得到 与
与 的等量关系,通过观察三者之间的等量关系发现
的等量关系,通过观察三者之间的等量关系发现 、
、 、
、 三者满足勾股定理,最后在直角三角形中求出
三者满足勾股定理,最后在直角三角形中求出 的值;解法3是先求出
的值;解法3是先求出 的值,借助三角形的面积公式得出
的值,借助三角形的面积公式得出 与
与 之间的等量关系,再利用余弦定理最终得到
之间的等量关系,再利用余弦定理最终得到 与
与 的等量关系,最后利用三角形的面积公式求出
的等量关系,最后利用三角形的面积公式求出 的值;解法4是先求出
的值;解法4是先求出 的值,借助三角形的面积公式得出
的值,借助三角形的面积公式得出 与
与 之间的等量关系,从而得出
之间的等量关系,从而得出 与
与 的等量关系,并利用
的等量关系,并利用 得出
得出 和
和 的值,最后利用
的值,最后利用 求出
求出 的值.
的值.
试题解析:(1)由 ,得
,得 ,
, ,
, ,
, ,
, ,
,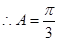 ;
;
(2)解法1: ,
, ,
, ,
,
由 ,得
,得 ,
,
由余弦定理得: ,
, ,
,
由正弦定理得: ,即
,即 ,
, .
.
解法2: ,
, ,
, ,
,
由 得
得 ,
,
由余弦定理得: ,
, ,
, ,
, 是直角三角形,角
是直角三角形,角 为直角,
为直角, ;
;
解法3: ,
, ,
, ,
,
由 得
得
由余弦定理得: ,
, ,
,
又 ,得
,得 ,
, ;
;
解法4: ,
, ,
, ,
,
由 得
得 ,
,
由正弦定理得:
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 +1=
+1= .
. )=
)= ,求sinA的值.
,求sinA的值. ,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
 ,求
,求 面积的最大值及此时
面积的最大值及此时 的值.
的值. ABC的三个内角A,B,C的对边,向量
ABC的三个内角A,B,C的对边,向量 =(sinA,1),
=(sinA,1), =(cosA,
=(cosA, ),且
),且 ,求
,求 中,
中, 分别为角
分别为角 的对边,且
的对边,且 .
. ).
). 的最大值,并写出
的最大值,并写出 ,b+c=2,求实数a的最小值。
,b+c=2,求实数a的最小值。 ,
, ,且
,且 .
. 时,求
时,求 ;
;  ,求函数
,求函数 的最值及相应的
的最值及相应的 的值.
的值. 的值
的值
 =
=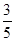 ,
, π<x<
π<x< π,求
π,求 的值.
的值.