题目内容
6、若集合M={y|y=x2,x∈Z},N={x|x2-6x-27≥0,x∈R},全集U=R,则M∩(?UN)的真子集的个数是( )
分析:通过解二次不等式化简集合N,求出N的补集,再求出M∩(?UN),据真子集个数的个数求出真子集的个数.
解答:解:∵N={x|x2-6x-27≥0}
={x|x≥9或x≤-3}.
∴?UN={x|-3<x<9},
∴M∩(?UN)={0,1,4}.
∴M∩(?UN)的真子集的个数为23-1=7.
故选B
={x|x≥9或x≤-3}.
∴?UN={x|-3<x<9},
∴M∩(?UN)={0,1,4}.
∴M∩(?UN)的真子集的个数为23-1=7.
故选B
点评:本题考查交集、补集、并集的混合运算;集合的真子集个数个数是2n-1.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
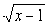 },则M∩P等于 ( )
},则M∩P等于 ( ) ,则M∩P=( )
,则M∩P=( ) ,则M∩P=( )
,则M∩P=( ) ,则M∩P=( )
,则M∩P=( )