题目内容
12.已知x为实数,y为正实数,集合A={x2+x+1,-x,-x-1},B={-y,-$\frac{y}{2}$,y+1},若A=B,求x2+y2的值.分析 由已知中x∈R,y∈R+,集合A={x2+x+1,-x,-x-1},B={-y,-$\frac{y}{2}$,y+1},A=B,求出满足条件的x,y值,进而可得答案.
解答 解:集合A={x2+x+1,-x,-x-1},B={-y,-$\frac{y}{2}$,y+1},
由x2+x+1>0恒成立,y∈R+得:
x2+x+1=y+1,
则-x-(-x-1)=-$\frac{y}{2}$-(-y)=$\frac{y}{2}$,
即1=$\frac{y}{2}$,
解得:y=2,
则B={-2,-1,3}
则x=1,A={-2,-1,3}满足条件,
故x2+y2=5.
点评 本题考查的知识点是集合的相等,分类讨论思想,难度中档.

练习册系列答案
相关题目
20.已知函数f(x)=$\frac{1}{2}$sin(2x+$\frac{π}{6}$),若f(x-φ)为偶函数,则φ可以为( )
| A. | $\frac{π}{2}$ | B. | -$\frac{π}{3}$ | C. | -$\frac{π}{6}$ | D. | $\frac{π}{6}$ |
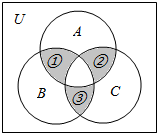 如图所示,已知全集U,用集合A、B、C及其交集、并集、补集的运算表示出图中的阴影部分.
如图所示,已知全集U,用集合A、B、C及其交集、并集、补集的运算表示出图中的阴影部分.