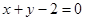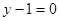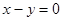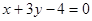题目内容
直线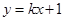 与圆
与圆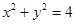 相交于A、B两点,则
相交于A、B两点,则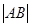 的最小值是( )
的最小值是( )
A. 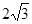 B.
B.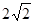 C.2 D. 1
C.2 D. 1
A;
解析试题分析:∵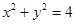 的圆心O(0,0),半径r=2,∴直线
的圆心O(0,0),半径r=2,∴直线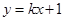 必过点(0,1),则点(0,1)到圆心O(0,0)的距离d=1,∴点(0,1)在圆内.
必过点(0,1),则点(0,1)到圆心O(0,0)的距离d=1,∴点(0,1)在圆内.
如图,
|AB|最小时,弦心距最大为1,∴ 故答案为:A.
故答案为:A.
考点:两点间的距离公式.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
圆 的半径为 ( )
的半径为 ( )
A. | B.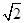 | C. | D.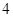 |
圆C的圆心在y轴正半轴上,且与x轴相切,被双曲线 的渐近线截得的弦长为
的渐近线截得的弦长为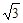 ,则圆C的方程为( )
,则圆C的方程为( )
| A.x2+(y-1)2=1 | B.x2+(y-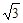 )2=3 )2=3 |
C.x2+(y- )2= )2= | D.x2+(y-2)2=4 |
已知 满足
满足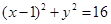 ,则
,则 的最小值为( )
的最小值为( )
| A.3 | B.5 | C.9 | D.25 |
过点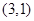 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为 ,
, ,则直线
,则直线 的方程为( )
的方程为( )
| A.2x+y-3=0 | B.2x-y-3="0" | C.4x-y-3=0 | D.4x+y-3=0 |
将圆 平分的直线的方程可以是 ( )
平分的直线的方程可以是 ( )
A.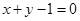 | B.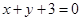 | C. | D.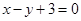 |
已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程为( )
| A.(x+1)2+y2=2 | B.(x-1)2+y2=1 |
| C.(x+1)2+y2=4 | D.(x-2)2+y2=4 |
当a为任意实数时,直线(a-1)x-y+a+1=0恒过定点C,则以C为圆心,半径为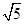 的圆的方程为( ).
的圆的方程为( ).
| A.x2+y2-2x+4y=0 |
| B.x2+y2+2x+4y=0 |
| C.x2+y2+2x-4y=0 |
| D.x2+y2-2x-4y=0 |
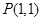 的直线将圆形区域
的直线将圆形区域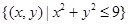 分成两部分,使得两部分的面积相差最大,则该直线的方程是( )
分成两部分,使得两部分的面积相差最大,则该直线的方程是( )