题目内容
【题目】已知定点F(1,0),定直线![]() ,动点M到点F的距离与到直线l的距离相等.
,动点M到点F的距离与到直线l的距离相等.
(1)求动点M的轨迹方程;
(2)设点![]() ,过点F作一条斜率大于0的直线交轨迹M于A,B两点,分别连接PA,PB,若直线PA与直线PB不关于x轴对称,求实数t的取值范围.
,过点F作一条斜率大于0的直线交轨迹M于A,B两点,分别连接PA,PB,若直线PA与直线PB不关于x轴对称,求实数t的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用抛物线定义可知:动点![]() 的轨迹为抛物线,从而得到动点M的轨迹方程;
的轨迹为抛物线,从而得到动点M的轨迹方程;
(2)过点![]() 的直线方程可设为
的直线方程可设为![]() 代入
代入![]() 可得
可得![]() ,利用韦达定理表示
,利用韦达定理表示![]() ,即可得到结果.
,即可得到结果.
(1)由题可知,动点![]() 的轨迹为抛物线,其焦点在
的轨迹为抛物线,其焦点在![]() 轴上,且
轴上,且![]() .
.
所以动点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)过点![]() 的直线方程可设为
的直线方程可设为![]() ,
,
联立方程组![]() .
.
设![]() ,
,
所以![]()
所以![]()
而![]()
![]() ,
,
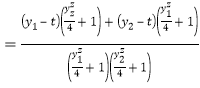 ,
,
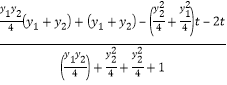 ,2
,2
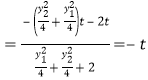 ,
,
当![]() 时,
时,![]() ,此时直线
,此时直线![]() 关于
关于![]() 轴对称,
轴对称,
当![]() 时,
时,![]() ,此时直线
,此时直线![]() 不关于
不关于![]() 轴对称。
轴对称。
所以实数t的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某科研机构为了研究喝酒与糖尿病是否有关,现对该市30名男性成人进行了问卷调查,并得到了如下列联表,规定“平均每天喝100ml以上的”为常喝.已知在所有的30人中随机抽取1人,是糖尿病的概率为![]() .
.
常喝 | 不常喝 | 合计 | |
有糖尿病 | 2 | ||
无糖尿病 | 18 | ||
合计 | 30 |
(1)请将上表补充完整;
(2)是否有![]() 的把握认为糖尿病与喝酒有关?请说明理由.
的把握认为糖尿病与喝酒有关?请说明理由.
(3)已知常喝酒且有糖尿病的人中恰有两名女性,现从常喝酒且有糖尿病的人中随机抽取2人,求恰好抽到一名男性和一名女性的概率.
参考公式:
参考数据:
|
|
|
|
|
|
| |
k |
|
|
|
|
|
|
|