题目内容
已知关于x的方程log3(x-1)-k=0在区间[2,10]上有实数根,那么k的取值范围是______.
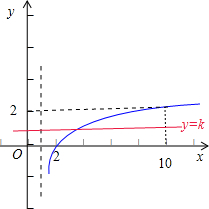
方法一:由题意可得,函数y=log3(x-1)的图象
和直线y=k在区间[2,10]上有交点,
如图所示:
数形结合可得 0≤k≤2,
故答案为[0,2].
方法二:由关于x的方程log3(x-1)-k=0,
可得k=log3(x-1),
且此函数在其定义域(1,+∞)上是增函数.
再由x∈[2,10],可得 log3(2-1)≤k≤log3(10-1),
即0≤k≤2,
故答案为:[0,2].
和直线y=k在区间[2,10]上有交点,
如图所示:
数形结合可得 0≤k≤2,
故答案为[0,2].
方法二:由关于x的方程log3(x-1)-k=0,
可得k=log3(x-1),
且此函数在其定义域(1,+∞)上是增函数.
再由x∈[2,10],可得 log3(2-1)≤k≤log3(10-1),
即0≤k≤2,
故答案为:[0,2].


练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目






 ;②
;② ;③
;③ ;④
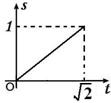
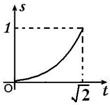
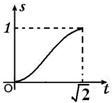
;④ 的图象(部分)如下:
的图象(部分)如下: