题目内容
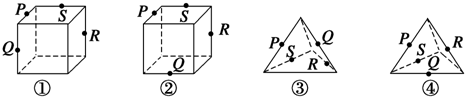
下列如图所示是正方体和正四面体，P、Q、R、S分别是所在棱的中点，则四个点共面的图形是
①③
①③
．分析：由中点构成的中位线和几何体的特征先判断是否平行，再判断是否在同一个平面内．
解答：解：①由题意知在正方体中，PS和QR都和上底的对角线平行，所以PS∥QR，则P、Q、R、S四个点共面，所以正确．
②由题意知在正方体中，PQ和SR是异面直线，则P、Q、R、S四个点不共面，所以错误．
③因PQ和RS分别是相邻侧面的中位线，所以PQ∥SQ，所以P、Q、R、S四个点共面，所以正确．
④根据图中几何体得，PQ和SR是异面直线，则P、Q、R、S四个点不共面，所以错误．
故答案为：①③．
②由题意知在正方体中，PQ和SR是异面直线，则P、Q、R、S四个点不共面，所以错误．
③因PQ和RS分别是相邻侧面的中位线，所以PQ∥SQ，所以P、Q、R、S四个点共面，所以正确．
④根据图中几何体得，PQ和SR是异面直线，则P、Q、R、S四个点不共面，所以错误．
故答案为：①③．
点评：本题考查了公理以及推论的应用、棱柱和棱锥的结构特征，主要根据中点构成中位线的性质和几何体进行判断．
练习册系列答案
阅读快车系列答案
相关题目
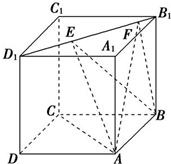如图所示，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E，F，且EF=
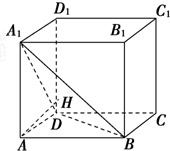14、如图所示，正方体ABCD-A1B1C1D1的棱长是1，过A点作平面A1BD的垂线，垂足为点H，有下列三个命题：
