Question

从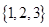中随机地选取一个数a，从中随机地选取一个数b，从中随机地选取一个数c，则a,b,c成等差数列的概率是        。

Answer 1

解析试题分析：因为对于a,b,c的选择分别所有3，2，2，那么按照分步乘法计数原理可知，所有的情况有种，而满足事件A：a,b,c成等差数列的情况有必须a+c为偶数，则1+7=4+4,2+6=4+4,3+7=5+5，共有三种，那么根据古典概型概率可知答案为。
考点：本试题考查了古典概型概率的求解运用。
点评：解决该试题的关键是弄清楚所有的基本事件数，也就是a,b的有序数对共有多少种，同时研究是事件为a,b,c成等差数列，解2b=a+c,结合已知中的数字来分析得到基本事件的数目，然后结合古典概型概率的公式进行求解运用。属于基础题。