题目内容
设n∈N*，不等式组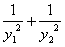
所表示的平面区域为Dn，把Dn内的整点（横、纵坐标均为整数的点）按其到原点的距离从近到远排列成点列：(x1,y1),(x2,y2),…,(xn,yn).
（1）求(xn,yn)；
（2）设数列{an}满足a1=x1,an=yn2(
+
+…+
)(n≥2),求证：n≥2时，
；
（3）在（2a）的条件下，比较(1+
)(1+
)…(1+
)与4的大小.
解:（1）由-nx+2n＞0及x＞0得0＜x＜2，因为x∈N*，所以x=1.
又x=1与y=-nx+2n的交点为(1,n)，所以Dn内的整点，按由近到远排列为：
（1，1），（1，2），…，(1,n).
（2）证明：n≥2时，an=yn2(+…+)=n2［++…+］.
所以=++…+
，
=
+
+…
.
两式相减得
=
.
（3）n=1时，1+
=2＜4，n=2时，(1+
)(1+
)=
＜4.
可猜想：n∈N*时，(1+
)(1+
)…(1+
)＜4,
事实上n≥3时，由（2）知
.
所以(1+
)(1+
)…(1+
)=
·
·
·…·
=
·
·(
·
·…·
)·(1+an)
=2·
·(
)2·(
)2·…·(
)2·(
)2·an+1
=
=2(
+
+
+…+
)
＜2［1+
+
+…+
］=2(1+1
+
+…+
)＜4.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
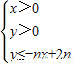所表示的平面区域为Dn，把Dn内的整点（横、纵坐标均为整数的点）按其到原点的距离从近到远排列成点列：（x1，y1），（x2，y2），…，（xn，yn）
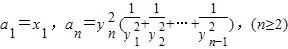，求证：n≥2时，
；
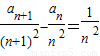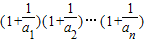与4的大小．
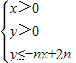所表示的平面区域为Dn，把Dn内的整点（横、纵坐标均为整数的点）按其到原点的距离从近到远排列成点列：（x1，y1），（x2，y2），…，（xn，yn）
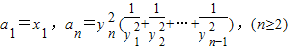，求证：n≥2时，
；
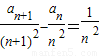与4的大小．