题目内容
设n∈N*,不等式组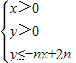 所表示的平面区域为Dn,把Dn内的整点(横、纵坐标均为整数的点)按其到原点的距离从近到远排列成点列:(x1,y1),(x2,y2),…,(xn,yn)
所表示的平面区域为Dn,把Dn内的整点(横、纵坐标均为整数的点)按其到原点的距离从近到远排列成点列:(x1,y1),(x2,y2),…,(xn,yn)(1)求(xn,yn);
(2)设数列{an}满足
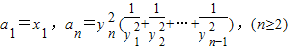 ,求证:n≥2时,
,求证:n≥2时,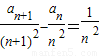 ;
;(3)在(2)的条件下,比较
 与4的大小.
与4的大小.
【答案】分析:(1)由-nx+2n>0及x>0得0<x<2,因为x∈N*,所以x=1,从而x=1与y=-nx+2n的交点为(1,n),即所以Dn内的整点(xn,yn)为(1,n)
(2)先化简为 ,两式相减即可证得
,两式相减即可证得
(3)先猜想:n∈N*时,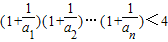 ,再利用(2)的结论可以证明.
,再利用(2)的结论可以证明.
解答:解:(1)由-nx+2n>0及x>0得0<x<2,因为x∈N*,所以x=1
又x=1与y=-nx+2n的交点为(1,n),所以Dn内的整点,按由近到远排列为:
(1,1),(1,2),…,(1,n)------------------(4分)
(2)证明:n≥2时,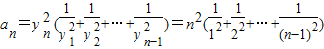
所以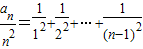 ,
,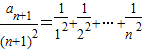
两式相减得: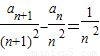 ------------------(9分)
------------------(9分)
(3)n=1时,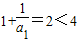 ,n=2时,
,n=2时,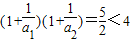
可猜想:n∈N*时,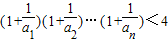 ------------------(11分)
------------------(11分)
事实上n≥3时,由(2)知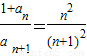
所以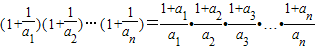
=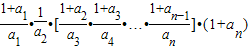
=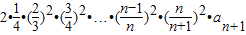
=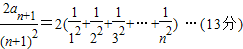
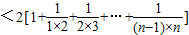
=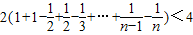 -----(15分)
-----(15分)
点评:本题以线性规划为载体,考查数列、不等式的证明,应注意充分挖掘题目的条件,合理转化
(2)先化简为
 ,两式相减即可证得
,两式相减即可证得(3)先猜想:n∈N*时,
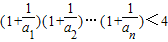 ,再利用(2)的结论可以证明.
,再利用(2)的结论可以证明.解答:解:(1)由-nx+2n>0及x>0得0<x<2,因为x∈N*,所以x=1
又x=1与y=-nx+2n的交点为(1,n),所以Dn内的整点,按由近到远排列为:
(1,1),(1,2),…,(1,n)------------------(4分)
(2)证明:n≥2时,
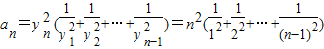
所以
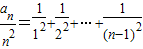 ,
,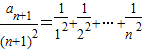
两式相减得:
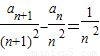 ------------------(9分)
------------------(9分)(3)n=1时,
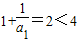 ,n=2时,
,n=2时,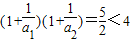
可猜想:n∈N*时,
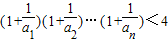 ------------------(11分)
------------------(11分)事实上n≥3时,由(2)知
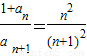
所以
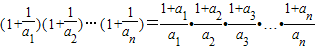
=
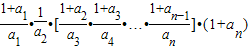
=
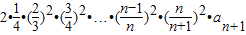
=
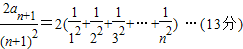
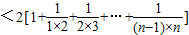
=
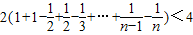 -----(15分)
-----(15分)点评:本题以线性规划为载体,考查数列、不等式的证明,应注意充分挖掘题目的条件,合理转化

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
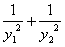 所表示的平面区域为Dn,把Dn内的整点(横、纵坐标均为整数的点)按其到原点的距离从近到远排列成点列:(x1,y1),(x2,y2),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横、纵坐标均为整数的点)按其到原点的距离从近到远排列成点列:(x1,y1),(x2,y2),…,(xn,yn).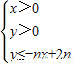 所表示的平面区域为Dn,把Dn内的整点(横、纵坐标均为整数的点)按其到原点的距离从近到远排列成点列:(x1,y1),(x2,y2),…,(xn,yn)
所表示的平面区域为Dn,把Dn内的整点(横、纵坐标均为整数的点)按其到原点的距离从近到远排列成点列:(x1,y1),(x2,y2),…,(xn,yn)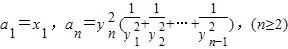 ,求证:n≥2时,
,求证:n≥2时,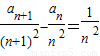 ;
;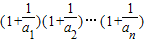 与4的大小.
与4的大小.