��Ŀ����
��n��N*������ʽ��
����ʾ��ƽ������ΪDn����Dn�ڵ����㣨�ᡢ�������Ϊ�����ĵ㣩���䵽ԭ��ľ���ӽ���Զ���гɵ��У���x1��y1������x2��y2����������xn��yn��
��1����xn��yn����
��2��������{an}����a1=x1��an=
(
+
+��+
)��(n��2)����֤��n��2ʱ��
-
=
��
��3���ڣ�2���������£��Ƚ�(1+
)(1+
)��(1+
)��4�Ĵ�С��
|
��1����xn��yn����
��2��������{an}����a1=x1��an=
| y | 2 n |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| an+1 | ||
(n+1
|
| an | ||
|
| 1 | ||
|
��3���ڣ�2���������£��Ƚ�(1+
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
��������1����-nx+2n��0��x��0��0��x��2����Ϊx��N*������x=1���Ӷ�x=1��y=-nx+2n�Ľ���Ϊ��1��n����������Dn�ڵ����㣨xn��yn��Ϊ��1��n��
��2���Ȼ���Ϊ
=
+
+��+
����ʽ�������֤��
��3���Ȳ��룺n��N*ʱ��(1+
)(1+
)��(1+
)��4�������ã�2���Ľ��ۿ���֤����
��2���Ȼ���Ϊ
| an |
| n2 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
(n-1
|
��3���Ȳ��룺n��N*ʱ��(1+
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
����⣺��1����-nx+2n��0��x��0��0��x��2����Ϊx��N*������x=1
��x=1��y=-nx+2n�Ľ���Ϊ��1��n��������Dn�ڵ����㣬���ɽ���Զ����Ϊ��
��1��1������1��2����������1��n��------------------��4�֣�
��2��֤����n��2ʱ��an=
(
+
+��+
)=n2(
+
+��+
)
����
=
+
+��+
��
=
+
+��+
��ʽ����ã�
-
=
------------------��9�֣�
��3��n=1ʱ��1+
=2��4��n=2ʱ��(1+
)(1+
)=
��4
�ɲ��룺n��N*ʱ��(1+
)(1+
)��(1+
)��4------------------��11�֣�
��ʵ��n��3ʱ���ɣ�2��֪
=
����(1+
)(1+
)��(1+
)=
•
•
•��•
=
•
•[
•
•��•
]•(1+an)
=2•
•(
)2•(
)2•��•(
)2•(
)2•an+1
=
=2(
+
+
+��+
) ��(13��)
��2[1+
+
+��+
]
=2(1+1-
+
-
+��+
-
)��4-----��15�֣�
��x=1��y=-nx+2n�Ľ���Ϊ��1��n��������Dn�ڵ����㣬���ɽ���Զ����Ϊ��
��1��1������1��2����������1��n��------------------��4�֣�
��2��֤����n��2ʱ��an=
| y | 2 n |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
(n-1
|
����
| an |
| n2 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
(n-1
|
| an+1 |
| (n+1)2 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
��ʽ����ã�
| an+1 | ||
(n+1
|
| an | ||
|
| 1 | ||
|
��3��n=1ʱ��1+
| 1 |
| a1 |
| 1 |
| a1 |
| 1 |
| a2 |
| 5 |
| 2 |
�ɲ��룺n��N*ʱ��(1+
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
��ʵ��n��3ʱ���ɣ�2��֪
| 1+an | ||
|
| n2 | ||
(n+1
|
����(1+
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 1+a1 |
| a1 |
| 1+a2 |
| a2 |
| 1+a3 |
| a3 |
| 1+an |
| an |
=
| 1+a1 |
| a1 |
| 1 |
| a2 |
| 1+a2 |
| a3 |
| 1+a3 |
| a4 |
| 1+an-1 |
| an |
=2•
| 1 |
| 4 |
| 2 |
| 3 |
| 3 |
| 4 |
| n-1 |
| n |
| n |
| n+1 |
=
| 2an+1 |
| (n+1)2 |
| 1 |
| 12 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
��2[1+
| 1 |
| 1��2 |
| 1 |
| 2��3 |
| 1 |
| (n-1)��n |
=2(1+1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
���������������Թ滮Ϊ���壬�������С�����ʽ��֤����Ӧע�����ھ���Ŀ������������ת��

��ϰ��ϵ�д�
�����Ŀ
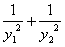 ����ʾ��ƽ������ΪDn����Dn�ڵ����㣨�ᡢ�������Ϊ�����ĵ㣩���䵽ԭ��ľ���ӽ���Զ���гɵ��У�(x1,y1),(x2,y2),��,(xn,yn).
����ʾ��ƽ������ΪDn����Dn�ڵ����㣨�ᡢ�������Ϊ�����ĵ㣩���䵽ԭ��ľ���ӽ���Զ���гɵ��У�(x1,y1),(x2,y2),��,(xn,yn).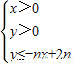 ����ʾ��ƽ������ΪDn����Dn�ڵ����㣨�ᡢ�������Ϊ�����ĵ㣩���䵽ԭ��ľ���ӽ���Զ���гɵ��У���x1��y1������x2��y2����������xn��yn��
����ʾ��ƽ������ΪDn����Dn�ڵ����㣨�ᡢ�������Ϊ�����ĵ㣩���䵽ԭ��ľ���ӽ���Զ���гɵ��У���x1��y1������x2��y2����������xn��yn��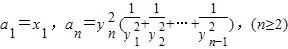 ����֤��n��2ʱ��
����֤��n��2ʱ��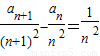 ��
��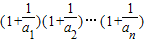 ��4�Ĵ�С��
��4�Ĵ�С��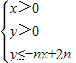 ����ʾ��ƽ������ΪDn����Dn�ڵ����㣨�ᡢ�������Ϊ�����ĵ㣩���䵽ԭ��ľ���ӽ���Զ���гɵ��У���x1��y1������x2��y2����������xn��yn��
����ʾ��ƽ������ΪDn����Dn�ڵ����㣨�ᡢ�������Ϊ�����ĵ㣩���䵽ԭ��ľ���ӽ���Զ���гɵ��У���x1��y1������x2��y2����������xn��yn��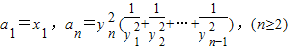 ����֤��n��2ʱ��
����֤��n��2ʱ��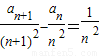 ��
�� ��4�Ĵ�С��
��4�Ĵ�С��