题目内容
已知a，b，c为正实数，a+b+c=1. 求证:
(1)a2+b2+c2≥
(2)
≤6
证明略
解析:
(1)证法一:a2+b2+c2－
=(3a2+3b2+3c2－1)
=［3a2+3b2+3c2－(a+b+c)2］
=［3a2+3b2+3c2－a2－b2－c2－2ab－2ac－2bc］
=［(a－b)2+(b－c)2+(c－a)2］≥0 ∴a2+b2+c2≥
证法二:∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
≤a2+b2+c2+a2+b2+a2+c2+b2+c2
∴3(a2+b2+c2)≥(a+b+c)2=1 ∴a2+b2+c2≥
证法三: ∵
∴a2+b2+c2≥
∴a2+b2+c2≥
证法四： 设a=+α，b=+β，c=+γ.
∵a+b+c=1，∴α+β+γ=0
∴a2+b2+c2=(+α)2+(+β)2+(+γ)2
=+
(α+β+γ)+α2+β2+γ2
=+α2+β2+γ2≥
∴a2+b2+c2≥
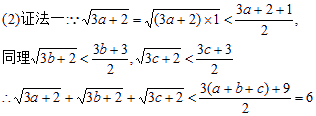
∴原不等式成立.
证法二： 
∴
≤
＜6
∴原不等式成立.
练习册系列答案
超能学典应用题题卡系列答案
相关题目