题目内容
已知a,b,c为正整数,方程ax2+bx+c=0的两实根为x1,x2(x1≠x2),且|x1|<1,|x2|<1,则a+b+c的最小值为______.
依题意,可知
从而可知x1,x2∈(-1,0),
所以有
?
又a,b,c为正整数,取c=1,则a+1>b?a≥b,
所以a2≥b2>4ac=4a?a>4.从而a≥5,所以b2>4ac≥20.
又b<5+1=6,所以b=5,因此a+b+c有最小值为11.
下面可证c≥2时,a≥3,从而b2>4ac≥24,所以b≥5.
又a+c>b≥5,所以a+c≥6,所以a+b+c≥11.
综上可得,a+b+c的最小值为11.
故答案为:11
|
所以有
|
|
所以a2≥b2>4ac=4a?a>4.从而a≥5,所以b2>4ac≥20.
又b<5+1=6,所以b=5,因此a+b+c有最小值为11.
下面可证c≥2时,a≥3,从而b2>4ac≥24,所以b≥5.
又a+c>b≥5,所以a+c≥6,所以a+b+c≥11.
综上可得,a+b+c的最小值为11.
故答案为:11

练习册系列答案
相关题目
已知函数f(x)=3sin2![]() +1,则使得f(x+c)=f(x)恒成立的c的最小正整数值为
+1,则使得f(x+c)=f(x)恒成立的c的最小正整数值为
[ ]
|
A.1 |
B.2 |
|
C.3 |
D.4 |
 (2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.
(2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.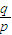 ,其中p、q均为整数且p、q互质)
,其中p、q均为整数且p、q互质)
 ,其中p、q均为整数且p、q互质)
,其中p、q均为整数且p、q互质)