题目内容
1.设等差数列{an}的前n项和为Sn,已知(a4-1)3+2016(a4-1)=1,(a2013-1)3+2016(a2013-1)=-1,则下列结论正确的是( )| A. | S2016=-2016,a2013>a4 | B. | S2016=2016,a2013>a4 | ||
| C. | S2016=-2016,a2013<a4 | D. | S2016=2016,a2013<a4 |
分析 y由a4-1)3+2016(a4-1)=1,(a2013-1)3+2016(a2013-1)=-1,设a4-1=m,a2013-1=n.即m3+2016m+n3+2016n=0,化为(m+n)(m2+n2-mn+2016)=0,可得m+n=0.即a4+a2013=2.再利用等差数列的性质与前n项和公式即可得出.
解答 解:∵(a4-1)3+2016(a4-1)=1,(a2013-1)3+2016(a2013-1)=-1,
∴(a4-1)3+2016(a4-1)+(a2013-1)3+2016(a2013-1)=0,
设a4-1=m,a2013-1=n.
则m3+2016m+n3+2016n=0,
化为(m+n)(m2+n2-mn+2016)=0,
∵m2+n2-mn+2016>0,
∴m+n=a4-1+a2013-1=0.
∴a4+a2013=2.
∴S2016=$\frac{2016({a}_{1}+{a}_{2016})}{2}$=$\frac{2016({a}_{4}+{a}_{2013})}{2}$=2016.
又a4-1>0,a2013-1<0.
∴a4>1>a2013,
故选:D.
点评 本题考查了等差数列的性质与前n项和公式、乘法公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
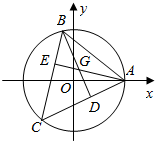 如图,点A(2,0)是一定点,定圆的方程是x2+y2=4,在定圆上取两点B、C,使得∠BAC=$\frac{π}{3}$,求△ABC的垂心G的轨迹方程.
如图,点A(2,0)是一定点,定圆的方程是x2+y2=4,在定圆上取两点B、C,使得∠BAC=$\frac{π}{3}$,求△ABC的垂心G的轨迹方程.