题目内容
已知函数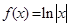
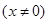 ,函数
,函数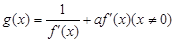
⑴当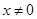 时,求函数
时,求函数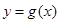 的表达式;
的表达式;
⑵若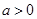 ,函数
,函数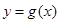 在
在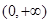 上的最小值是2 ,求
上的最小值是2 ,求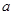 的值;
的值;
(1)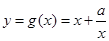 (2)
(2)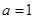 .
.
解析试题分析:(1)分情况讨论x的取值化简绝对值,求出f′(x)得到x>0和x<0导函数相等,代入到g(x)中得到即可;
(2)根据基本不等式得到g(x)的最小值即可求出a.
试题解析:解:⑴∵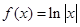 ,
,
∴当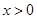 时,
时,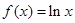 ; 当
; 当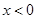 时,
时,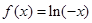
∴当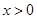 时,
时,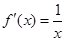 ; 当
; 当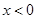 时,
时,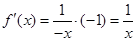 .
.
∴当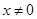 时,函数
时,函数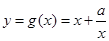 .6分
.6分
⑵∵由⑴知当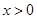 时,
时,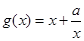 ,
,
∴当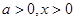 时,
时, 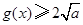 当且仅当
当且仅当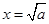 时取等号 8分
时取等号 8分
∴函数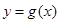 在
在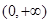 上的最小值是
上的最小值是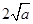 ,∴依题意得
,∴依题意得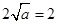 ∴
∴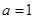 ; 12分
; 12分
考点:1.函数的最值及其几何意义;2.导数的运算.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 与日产量
与日产量 (件)之间近似地满足关系式
(件)之间近似地满足关系式 (日产品废品率
(日产品废品率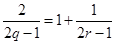
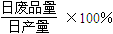 ).已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润
).已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润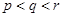 日正品赢利额
日正品赢利额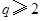 日废品亏损额)
日废品亏损额)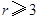 (千元)表示为日产量
(千元)表示为日产量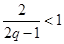 (件)的函数;
(件)的函数;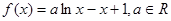 .
. 的单调区间;
的单调区间;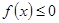 在
在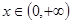 上恒成立,求所有实数
上恒成立,求所有实数 的值;
的值;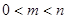 ,证明:
,证明: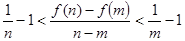
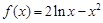
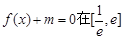 内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)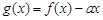 的图象与x轴交于两点
的图象与x轴交于两点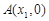 、
、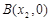 且
且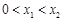 .求证:
.求证: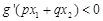 (其中正常数
(其中正常数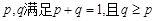 ).
).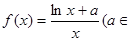 R).
R).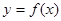 在点
在点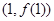 处的切线与直线
处的切线与直线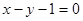 平行,求
平行,求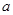 的值;
的值; 的单调区间和极值;
的单调区间和极值;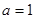 ,且
,且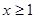 时,证明:
时,证明: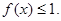
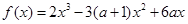
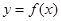 在点(2,f (2))处的切线方程;
在点(2,f (2))处的切线方程;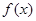 在闭区间[0,|2a|]上的最小值.
在闭区间[0,|2a|]上的最小值.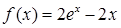 ,
,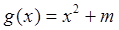 (
(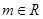 ).
).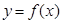 的单调性;
的单调性;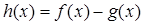 ,
,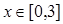 ,当函数
,当函数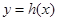 有零点时,求实数
有零点时,求实数 的最大值.
的最大值.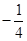 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;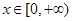 时,函数y=f(x)图像上的点都在
时,函数y=f(x)图像上的点都在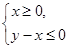 所表示的平面区域内,求实数a的取值范围;
所表示的平面区域内,求实数a的取值范围;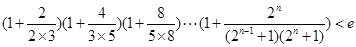 (其中
(其中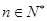 ,e是自然数对数的底数)
,e是自然数对数的底数)