题目内容
(1)在伸缩变换
下圆x2+y2=1变为曲线C.求曲线C的方程,并指出曲线的类型;当曲线C的动点M到直线L:
ρcosθ+2ρsinθ+5
=0距离的最大值时,求点M的坐标.
(2)设函数f(x)=|x+1|+|x-a|(a>0).
①作出函数f(x)的图象;
②若不等式f(x)≥5的解集为(-∞,-2]∪[3,+∞),求a值.
|
| 3 |
| 6 |
(2)设函数f(x)=|x+1|+|x-a|(a>0).
①作出函数f(x)的图象;
②若不等式f(x)≥5的解集为(-∞,-2]∪[3,+∞),求a值.
分析:(1)利用伸缩变换求出曲线C的方程,根据ρsinθ=y,ρcosθ=x,把极坐标方程化为普通方程得到直线l的方程,设出曲线C参数方程一点坐标,利用点到直线的距离公式表示出P到直线l的距离d,利用两角和的余弦函数公式化为一个角的余弦函数,根据余弦函数的值域即可求出d的最大值.
(2)①根据题意,化简绝对值可得,函数f(x)=|x+1|+|x-a|=
,进而做出其图象.
②由题设知:|x+1|+|x-a|≥5,在同一坐标系中作出函数y=5的图象,当x=-2或3时,f(x)=5,且a+1<5即a<4,由f(-2)=5 求得 a 的值.
(2)①根据题意,化简绝对值可得,函数f(x)=|x+1|+|x-a|=
|
②由题设知:|x+1|+|x-a|≥5,在同一坐标系中作出函数y=5的图象,当x=-2或3时,f(x)=5,且a+1<5即a<4,由f(-2)=5 求得 a 的值.
解答:解:(1)由x′=2x,y′=
y得x=
,y=
代入x2+y2=1
即曲线C:
+
=1.
该曲线是椭圆.其参数方程为:
(θ为参数)
设椭圆C上动点M(2cosθ,
sinθ),(0≤θ<2π)
到直线L:
x+2y+5
=0的距离为d=
=
≤
.
当θ=
时,曲线C的动点M到直线L的距离最大,此时M(
,
)…(7分)
(2)①f(x)=|x+1|+|x-a|=
,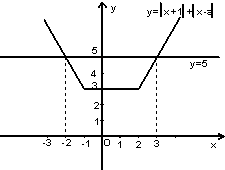
函数f(x)如图所示.
②由题设知:|x+1|+|x-a|≥5,
如图,在同一坐标系中作出函数y=5的图象
(如图所示)
又解集为(-∞,-2]∪[3,+∞).
由题设知,当x=-2或3时,f(x)=5
且a+1<5即a<4,
由f(-2)=-2(-2)-1+a=5得:a=2.
| 3 |
| x′ |
| 2 |
| y′ | ||
|
即曲线C:
| x2 |
| 4 |
| y2 |
| 3 |
该曲线是椭圆.其参数方程为:
|
设椭圆C上动点M(2cosθ,
| 3 |
到直线L:
| 3 |
| 6 |
|2
| ||||||
|
=
|2
| ||||||
|
| 42 |
当θ=
| π |
| 4 |
| 2 |
| ||
| 2 |
(2)①f(x)=|x+1|+|x-a|=
|

函数f(x)如图所示.
②由题设知:|x+1|+|x-a|≥5,
如图,在同一坐标系中作出函数y=5的图象
(如图所示)
又解集为(-∞,-2]∪[3,+∞).
由题设知,当x=-2或3时,f(x)=5
且a+1<5即a<4,
由f(-2)=-2(-2)-1+a=5得:a=2.
点评:本题考查伸缩变换、简单曲线的极坐标方程、绝对值不等式的解法,函数图象的特征,体现了数形结合的数学思想,第(2)小题画出函数f(x)的图象,是解题的关键.

练习册系列答案
相关题目
 本题有(1),(2),(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑.
本题有(1),(2),(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑.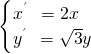 下圆x2+y2=1变为曲线C.求曲线C的方程,并指出曲线的类型;当曲线C的动点M到直线L:
下圆x2+y2=1变为曲线C.求曲线C的方程,并指出曲线的类型;当曲线C的动点M到直线L: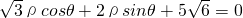 距离的最大值时,求点M的坐标.
距离的最大值时,求点M的坐标.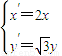 下圆x2+y2=1变为曲线C.求曲线C的方程,并指出曲线的类型;当曲线C的动点M到直线L:
下圆x2+y2=1变为曲线C.求曲线C的方程,并指出曲线的类型;当曲线C的动点M到直线L: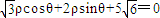 距离的最大值时,求点M的坐标.
距离的最大值时,求点M的坐标.