题目内容
在同一坐标系中,将圆x2+y2=4在伸缩变换
下的方程是( )
|
分析:由伸缩变换
得
,将此式代入原曲线方程即可得到经过伸缩变换
后的曲线方程.
|
|
|
解答:解:由伸缩变换
得
,
将此式代入曲线x2+y2=4,
得(
)2+(
)2=4,即
+
=4.
故选A.
|
|
将此式代入曲线x2+y2=4,
得(
| X |
| 2 |
| Y |
| 3 |
| X2 |
| 4 |
| Y2 |
| 9 |
故选A.
点评:此题考查按照伸缩变换
后得到的曲线方程,只要用X,Y表示x,y,再代入原曲线方程就可得到答案,较简单.
|

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目

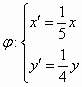
 下的方程是( )
下的方程是( )
