题目内容
已知定义在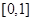 上的函数
上的函数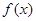 满足:
满足:
①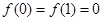 ;
;
②对所有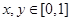 ,且
,且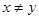 ,有
,有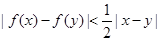 .
.
若对所有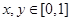 ,
, ,则k的最小值为( )
,则k的最小值为( )
A.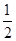 | B.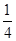 | C.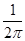 | D.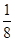 |
B
解析试题分析:不妨令 ,则
,则
法一:
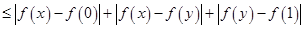
 ,
,
即得 ,
,
另一方面,当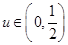 时,
时, ,符合题意,
,符合题意,
当 时,
时, ,
,
故
法二:当 时,
时,  ,
,
当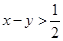 时,
时,
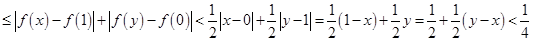 ,
,
故
考点:1.抽象函数问题;2.绝对值不等式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
不等式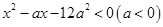 的解集是( )
的解集是( )
A.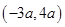 | B.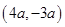 | C.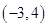 | D.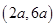 |
不等式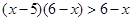 的解集是( )
的解集是( )
A.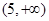 | B.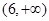 | C.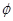 | D.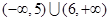 |
三个数a=0.32, 之间的大小关系是( )
之间的大小关系是( )
| A.b<c<a | B.c<b<a | C.b<a<c | D.a<c<b |
对一切实数x,不等式x2+a|x|+1≥0恒成立,则实数a的取值范围是( )
| A.[-2,+∞) | B.(-∞,-2) |
| C.[-2,2] | D.[0,+∞) |
已知正整数a,b满足4a+b=30,则使得 +
+ 取最小值时的实数对(a,b)
取最小值时的实数对(a,b)
是 ( )
| A.(5,10) | B.(6,6) |
| C.(10,5) | D.(7,2) |
设x,y∈R+,且满足x+4y=40,则lgx+lgy的最大值为 ( )
| A.40 | B.10 | C.4 | D.2 |
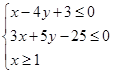
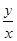 ,求z的最小值;
,求z的最小值;