题目内容
某中学号召学生在今年暑假期间至少参加一次社会公益活动(以下简称活动).该校学生会共有100名学生,他们参加活动的次数统计如下表:
| 次数 | 1 | 2 | 3 |
| 人数 | 10 | 40 | 50 |
(1)从样本任意选两名学生,求至少有一个参加了2次活动的概率;
(2)从样本任意选一名学生,若抽到的学生参加了2次活动,则抽取结束,若不是,则放回重聚,求恰好在第4次抽取后结束的概率.
解:(1)因参加活动1次、2次、3次的人数比例为10:40:50,即1:4:5; (1分)
故样本中参加活动1次、2次、3次的人数分别为1人、4人、5人 (2分)
记事件A为“恰有一人参加了2次活动”,事件B为“恰有两人参加了2次活动”,则A与B互斥. (3分)
故P(A)=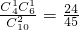 ,(4分)
,(4分)
P(B)=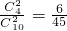 (5分)
(5分)
∴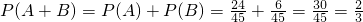
答:至少有一人参加了2次活动的概率为 . (6分)
. (6分)
(2)记事件C为“恰好在第4次抽取后结束”
每一次抽到参加了2次活动的学生的概率均为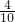 即
即 ,(1分)
,(1分)
抽到参加了1次或3次活动的学生的概率为 ,(2分)
,(2分)
依题即前3次均取到参加了1次或3次活动的学生,第4次取到参加了2次活动的学生 (3分)
∴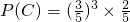 (4分)
(4分)
=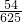 (5分)
(5分)
答:恰好在第4次抽取后结束的概率为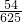 . (6分)
. (6分)
分析:(1)根据参加活动1次、2次、3次的人数比例为10:40:50,即1:4:5,得到样本中参加活动1次、2次、3次的人数分别为1人、4人、5人,“恰有一人参加了2次活动”和“恰有两人参加了2次活动两个事件之间互斥.
(2)每一次抽到参加了2次活动的学生的概率均为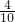 ,抽到参加了1次或3次活动的学生的概率为
,抽到参加了1次或3次活动的学生的概率为 ,依题即前3次均取到参加了1次或3次活动的学生,第4次取到参加了2次活动的学生,得到概率
,依题即前3次均取到参加了1次或3次活动的学生,第4次取到参加了2次活动的学生,得到概率
点评:本题考查等可能事件的概率,解题的关键是看出试验发生包含的事件和满足条件的事件数,写出事件数求比值即可.
故样本中参加活动1次、2次、3次的人数分别为1人、4人、5人 (2分)
记事件A为“恰有一人参加了2次活动”,事件B为“恰有两人参加了2次活动”,则A与B互斥. (3分)
故P(A)=
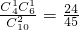 ,(4分)
,(4分)P(B)=
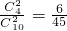 (5分)
(5分)∴
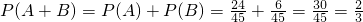
答:至少有一人参加了2次活动的概率为
 . (6分)
. (6分)(2)记事件C为“恰好在第4次抽取后结束”
每一次抽到参加了2次活动的学生的概率均为
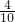 即
即 ,(1分)
,(1分)抽到参加了1次或3次活动的学生的概率为
 ,(2分)
,(2分)依题即前3次均取到参加了1次或3次活动的学生,第4次取到参加了2次活动的学生 (3分)
∴
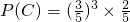 (4分)
(4分)=
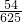 (5分)
(5分)答:恰好在第4次抽取后结束的概率为
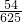 . (6分)
. (6分)分析:(1)根据参加活动1次、2次、3次的人数比例为10:40:50,即1:4:5,得到样本中参加活动1次、2次、3次的人数分别为1人、4人、5人,“恰有一人参加了2次活动”和“恰有两人参加了2次活动两个事件之间互斥.
(2)每一次抽到参加了2次活动的学生的概率均为
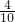 ,抽到参加了1次或3次活动的学生的概率为
,抽到参加了1次或3次活动的学生的概率为 ,依题即前3次均取到参加了1次或3次活动的学生,第4次取到参加了2次活动的学生,得到概率
,依题即前3次均取到参加了1次或3次活动的学生,第4次取到参加了2次活动的学生,得到概率点评:本题考查等可能事件的概率,解题的关键是看出试验发生包含的事件和满足条件的事件数,写出事件数求比值即可.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
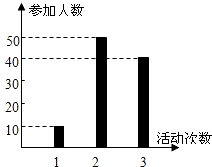 某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示. 某中学号召学生在今年暑假期间至少参加一次社会公益活动(以下简称活动).该校某班共有50名学生,他们参加的活动次数统计如图所示.
某中学号召学生在今年暑假期间至少参加一次社会公益活动(以下简称活动).该校某班共有50名学生,他们参加的活动次数统计如图所示.

 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 。
。