题目内容
 某中学号召学生在今年暑假期间至少参加一次社会公益活动(以下简称活动).该校某班共有50名学生,他们参加的活动次数统计如图所示.
某中学号召学生在今年暑假期间至少参加一次社会公益活动(以下简称活动).该校某班共有50名学生,他们参加的活动次数统计如图所示.(1)求该班学生参加活动的人均次数;
(2)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率.
分析:(1)由统计图可知,参加活动1次、2次和3次的学生人数,再根据平均数的求法,计算可得答案;
(2)根据题意,先由组合数公式计算从50名学生中任意选两名的情况数目,再用分类计数原理可得选出的2人参加活动次数不同的情况数目,由等可能事件的概率公式,计算可得他们参加活动次数不等的概率,最后利用对立事件的概率求得答案.
(2)根据题意,先由组合数公式计算从50名学生中任意选两名的情况数目,再用分类计数原理可得选出的2人参加活动次数不同的情况数目,由等可能事件的概率公式,计算可得他们参加活动次数不等的概率,最后利用对立事件的概率求得答案.
解答:解:(1)由图可知,参加活动1次、2次和3次的学生人数分别为5、25和20,
则该班学生参加活动的人均次数为
=2.3,
(2)该班共有50名学生,从中任意选两名学生,有
=1225种选法,
选出的2人参加活动次数不同的情况有
+
+
=725,
则他们参加活动次数不同的概率是
=
,
则他们参加活动次数恰好相等的概率为1-
=
.
则该班学生参加活动的人均次数为
| 1×5+2×25+3×20 |
| 50 |
(2)该班共有50名学生,从中任意选两名学生,有
| C | 2 50 |
选出的2人参加活动次数不同的情况有
| C | 1 5 |
| C | 1 25 |
| C | 1 5 |
| C | 1 20 |
| C | 1 25 |
| C | 1 20 |
则他们参加活动次数不同的概率是
| 725 |
| 1225 |
| 29 |
| 49 |
则他们参加活动次数恰好相等的概率为1-
| 29 |
| 49 |
| 20 |
| 49 |
点评:本题考查频数分布直方图的应用和等可能事件的概率计算,关键是利用统计图,获取信息,是基础题.

练习册系列答案
相关题目
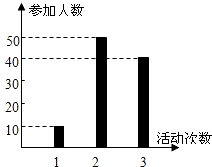 某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.

 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 。
。