题目内容
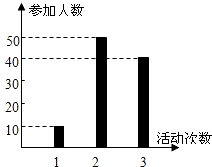某中学号召学生在今年春节期间至少参加一次社会公益活动（以下简称活动）．该校合唱团共有100名学生，他们参加活动的次数统计如图所示．（1）求合唱团学生参加活动的人均次数；
（2）从合唱团中任意选两名学生，求他们参加活动次数恰好相等的概率．
（3）从合唱团中任选两名学生，用ξ表示这两人参加活动次数之差的绝对值，求随机变量ξ的分布列及数学期望Eξ．
分析：（1）由图可知，参加活动1次、2次和3次的学生人数分别为10、50和40，根据平均数的求法，计算可得答案．
（2）欲求他们参加活动次数恰好相等的概率，频数分布直方图，清楚显示在各个不同区间内取值，各组频数分布情况，利用公式P0=
即可；
（3）ξ可能取值是：0，1，2．分别计算出取这此值时的概率即得分布列，再根据数学期望即可计算出结果．
（2）欲求他们参加活动次数恰好相等的概率，频数分布直方图，清楚显示在各个不同区间内取值，各组频数分布情况，利用公式P0=
| 10×9+50×49+39×40 |
| 100×99 |
（3）ξ可能取值是：0，1，2．分别计算出取这此值时的概率即得分布列，再根据数学期望即可计算出结果．
解答：解：由图可知，参加活动1次、2次和3次的学生人数分别为10、50和40．
（1）该合唱团学生参加活动的人均次数为
=
=2.3．
（2）从合唱团中任选两名学生，他们参加活动次数恰好相等的概率为
P0=
=
．
（3）从合唱团中任选两名学生，记“这两人中一人参加1次活动，另一人参加2次活动”为事件A，“这两人中一人参加2次活动，另一人参加3次活动”为事件B，“这两人中一人参加1次活动，另一人参加3次活动”为事件C．易知
P（ξ=1）=P（A）+P（B）=
+
=
；
P（ξ=2）=P（C）=
=
；
ξ的分布列：
ξ的数学期望：Eξ=0×
+1×
+2×
=
．
（1）该合唱团学生参加活动的人均次数为
| 1×10+2×50+3×40 |
| 100 |
| 230 |
| 100 |
（2）从合唱团中任选两名学生，他们参加活动次数恰好相等的概率为
P0=
| 10×9+50×49+39×40 |
| 100×99 |
| 41 |
| 99 |
（3）从合唱团中任选两名学生，记“这两人中一人参加1次活动，另一人参加2次活动”为事件A，“这两人中一人参加2次活动，另一人参加3次活动”为事件B，“这两人中一人参加1次活动，另一人参加3次活动”为事件C．易知
P（ξ=1）=P（A）+P（B）=
| ||||
|
| ||||
|
| 50 |
| 99 |
P（ξ=2）=P（C）=
| ||||
|
| 8 |
| 99 |
ξ的分布列：
ξ的数学期望：Eξ=0×
| 41 |
| 99 |
| 50 |
| 99 |
| 8 |
| 99 |
| 2 |
| 3 |
点评：考点：①求概率②求随机变量的分布列和期望，本题考查读频数分布直方图的能力和利用统计图获取信息的能力．利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
练习册系列答案
相关题目
某中学号召学生在今年暑假期间至少参加一次社会公益活动（以下简称活动）．该校某班共有50名学生，他们参加的活动次数统计如图所示．
表示这两人参加活动次数之差的绝对值，求随机变量
．
表示这两人参加活动次数之差的绝对值，求随机变量
。