题目内容
(本小题满分12分)如图,在正三棱柱![]() 中,点
中,点![]() 是棱
是棱![]() 的中点,
的中点,![]()
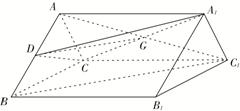 (Ⅰ)求证:
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角

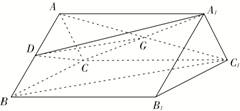
解: (1)证明:连结AC1交A1C于点G,连结DG,
在正三棱柱ABC—A1B1C1中,
四边形ACC1A1是平行四边形,
 ∴AG=GC1,
∴AG=GC1,
∵AD=DB,
∴DG//BC1 …………2分
∵DG![]() 平面A1DC,BC1
平面A1DC,BC1![]() 平面A1DC,
平面A1DC,
∴BC1//平面A1DC …………4分
(II)解法一:过D作DE⊥AC交AC于E,
 过点D作DF⊥A1C交A1C于F,连结EF。
过点D作DF⊥A1C交A1C于F,连结EF。
∵平面ABC⊥面平ACC1A1,DE![]() 平面ABC,
平面ABC,
平面ABC∩平面ACC1A1=AC,
∴DE⊥平ACC1A1,
∴EF是DF在平面ACC1A1内的射影。
∴EF⊥A1C,
∴∠DFE是二面角D—A1C—A的平面角, ………………8分
在直角三角形ADC中,![]()
同理可求:![]()
![]() ………………12分
………………12分
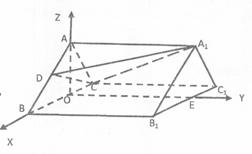
解法二:过点A作AO⊥BC交BC于O,过点O作OE⊥BC交B1C1于E。
因为平面ABC⊥平面CBB1C1 ,所以AO⊥平面CBB1C1,
分别以CB、OE、OA所在直线为x轴,y轴,z轴建立空间直角坐标系,如图所示
因为BC=1,AA1=![]() ,△ABC是等边三角形,所以O为BC的中点,则
,△ABC是等边三角形,所以O为BC的中点,则
![]() …………6分
…………6分
设平面A1DC的法向量为![]()
则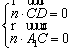

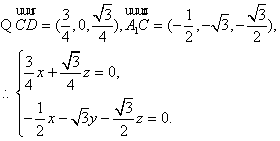
取![]() 得平面
得平面![]() 的一个法向量为
的一个法向量为![]() ………………8分
………………8分
可求平面ACA1的一个法向量为![]() ………………10分
………………10分
设二面角D—A1C—A的大小为![]() ,
,
则![]()
![]() ………………12分
………………12分

练习册系列答案
相关题目