Question

在△ABC中，角A，B，C所对的边分别为a，b，c，∠B=30°，c=6，记b=f（a），若函数g（a）=f（a）-k（k是常数）只有一个零点，则实数k的取值范围是（　　）

A．{k|0＜k≤3或k=6}

B．{k|3≤k≤6}

C．{k|k≥6}

D．{k|k≥6或k=3}

Answer 1

分析：由余弦定理可得 b=f（a）的解析式，利用二次函数的性质可得f（a）的最小值为3，f（a）的增区间为[3

3

，+∞），
减区间为（0，3

3

），且f（0）趋于6，由此可得实数k的取值范围．

解答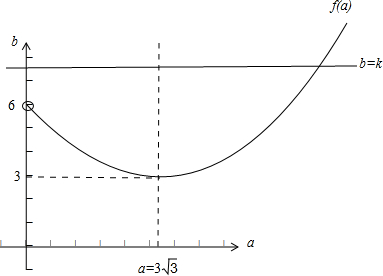：解：在△ABC中，∠B=30°，c=6，记b=f（a），
而由余弦定理可得 b=

a2+c2-2ac•cosB

=

a2+36-12a• 3 2

 
=

(a-3 3 )2+9

≥3，即f（a）的最小值为3．
由于函数g（a）=f（a）-k（k是常数）只有一个零点，故方函数y=f（a）与直线y=k有唯一交点，
由于函数f（a）的增区间为[3

3

，+∞），减区间为（0，3

3

），且f（0）趋于6，
结合函数b=f（a）的图象可得 k≥6，或k=3，
故选D．

点评：本题主要考查函数的零点与方程的根的关系，二次函数的性质应用，体现了转化的数学思想，属于基础题．