题目内容
4.现有四根长3cm、4cm、7cm、9cm的木棒,任取其中的三根,首尾相连后,能组成三角形的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
分析 列出基本事件,找出满足题意的个数,求解概率即可.
解答 解:现有四根长3cm、4cm、7cm、9cm的木棒,任取其中的三根,
共有3,4,7; 3,4,9; 3,7,9; 4,7,9;四种情况,能够组成三角形的有:3,7,9; 4,7,9;两种可能,
能组成三角形的概率为:$\frac{2}{4}$=$\frac{1}{2}$.
故选:D.
点评 本题考查古典概型的概率的求法,基本知识的考查.

练习册系列答案
相关题目
14.已知α为第二象限角,cos2α=-$\frac{\sqrt{5}}{3}$,则sinα-cosα=( )
| A. | $\frac{\sqrt{15}}{3}$ | B. | $\frac{\sqrt{15}}{3}$或$\frac{\sqrt{3}}{3}$ | C. | -$\frac{\sqrt{15}}{3}$ | D. | $\frac{\sqrt{3}}{9}$ |
16.已知A={x|x2<1},B={x|x≥0},全集U=R,则A∩(∁UB)=( )
| A. | {x|x<0} | B. | {x|x<-1} | C. | {x|-1<x<0} | D. | {x|0<x<1} |
1.对于二项展开式(a-b)2n+1,下列结论中成立的是( )
| A. | 中间一项的二项式系数最大 | B. | 中间两项的二项式系数相等且最大 | ||
| C. | 中间两项的二项式系数相等且最小 | D. | 中间两项的二项式系数互为相反数 |
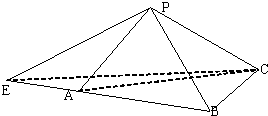 如图,在三棱锥P-ABC中,PA⊥平面PBC,PA=PB=2,PC=4,∠BPC=60°.
如图,在三棱锥P-ABC中,PA⊥平面PBC,PA=PB=2,PC=4,∠BPC=60°. 如图,在直四棱柱ABCD-A1B1C1D1中,四边形ABCD是直角梯形,∠DAB=90°,AA1=AB=BC=2,AD=1.
如图,在直四棱柱ABCD-A1B1C1D1中,四边形ABCD是直角梯形,∠DAB=90°,AA1=AB=BC=2,AD=1.