题目内容
设数列{an}是公比为a（a≠1），首项为b的等比数列，Sn是前n项和，对任意的n∈N+，点（Sn，Sn+1）在（ ）A．直线y=ax-b上
B．直线y=bx+a上
C．直线y=bx-a上
D．直线y=ax+b上
【答案】分析：利用等比数列的求和公式分别表示出Sn和Sn+1，代入选项的直线方程中验证即可．
解答：解：∵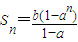
∴
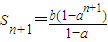
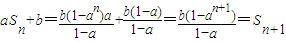
故点（Sn，Sn+1）在直线y=ax+b上，
故选D．
点评：本题主要考查了等比数列的性质，等比数列的求和公式．考查了考生对等比数列公式的记忆．
解答：解：∵
∴
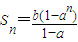
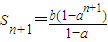
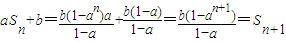
故点（Sn，Sn+1）在直线y=ax+b上，
故选D．
点评：本题主要考查了等比数列的性质，等比数列的求和公式．考查了考生对等比数列公式的记忆．
练习册系列答案
阅读快车系列答案
相关题目