题目内容
(本小题满分12分)函数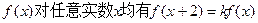 ,其中
,其中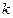 为已知的正常数,且
为已知的正常数,且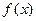 在区间[0,2]上有表达式
在区间[0,2]上有表达式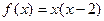 .
.
(1)求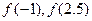 的值;
的值;
(2)求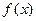 在[-2,2]上的表达式,并写出函数
在[-2,2]上的表达式,并写出函数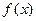 在[-2,2]上的单调区间(不需证明);
在[-2,2]上的单调区间(不需证明);
(3)求函数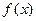 在[-2,2]上的最小值,并求出相应的自变量的值.
在[-2,2]上的最小值,并求出相应的自变量的值.
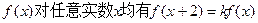 ,其中
,其中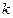 为已知的正常数,且
为已知的正常数,且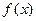 在区间[0,2]上有表达式
在区间[0,2]上有表达式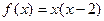 .
.(1)求
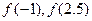 的值;
的值;(2)求
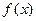 在[-2,2]上的表达式,并写出函数
在[-2,2]上的表达式,并写出函数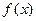 在[-2,2]上的单调区间(不需证明);
在[-2,2]上的单调区间(不需证明);(3)求函数
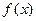 在[-2,2]上的最小值,并求出相应的自变量的值.
在[-2,2]上的最小值,并求出相应的自变量的值.解:(1)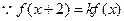
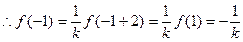 ,…………………………………………………1分
,…………………………………………………1分
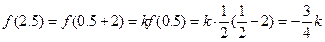 ……………………………………3分
……………………………………3分
(2)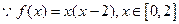 ,
,
设 ,
,
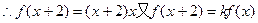
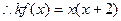
 ………………………………………………………………4分
………………………………………………………………4分
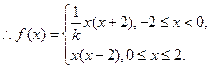 ………………………………………………………5分
………………………………………………………5分
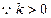 ,结合二次函数的图象得.
,结合二次函数的图象得.
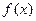 的减区间为
的减区间为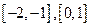 ……………………………………………………………6分
……………………………………………………………6分
增区间为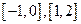 ………………………………………………………………………7分
………………………………………………………………………7分
(3)由函数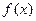 在
在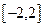 上的单调性知,
上的单调性知,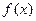 在
在 或
或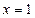 处取得极小值.
处取得极小值.
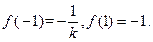 .…………………………………………………………………8分
.…………………………………………………………………8分
故有:①当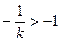 即
即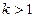 时,
时,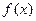 在
在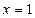 处取得最小值-1,
处取得最小值-1,
②当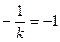 即
即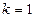 时,
时,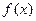 在
在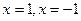 处都取得最小值-1.
处都取得最小值-1.
③当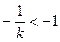 即
即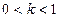 时,
时,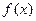 在
在 处取得最小值
处取得最小值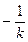 .……12分
.……12分
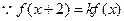
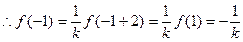 ,…………………………………………………1分
,…………………………………………………1分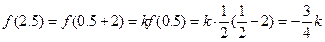 ……………………………………3分
……………………………………3分(2)
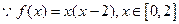 ,
,设
 ,
,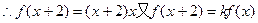
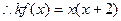
 ………………………………………………………………4分
………………………………………………………………4分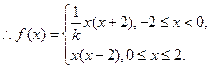 ………………………………………………………5分
………………………………………………………5分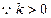 ,结合二次函数的图象得.
,结合二次函数的图象得.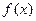 的减区间为
的减区间为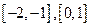 ……………………………………………………………6分
……………………………………………………………6分增区间为
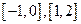 ………………………………………………………………………7分
………………………………………………………………………7分(3)由函数
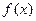 在
在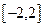 上的单调性知,
上的单调性知,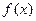 在
在 或
或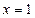 处取得极小值.
处取得极小值. 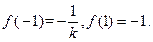 .…………………………………………………………………8分
.…………………………………………………………………8分故有:①当
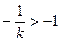 即
即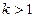 时,
时,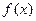 在
在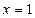 处取得最小值-1,
处取得最小值-1,②当
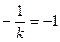 即
即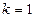 时,
时,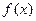 在
在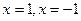 处都取得最小值-1.
处都取得最小值-1.③当
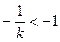 即
即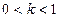 时,
时,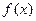 在
在 处取得最小值
处取得最小值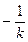 .……12分
.……12分略

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
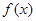 同时满足如下三个条件,求
同时满足如下三个条件,求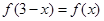 ;②
;②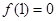 ;③对任意实数
;③对任意实数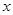 ,都有
,都有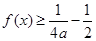 恒成立.
恒成立.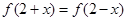 ,(2)被
,(2)被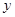 轴截距为6,求此函数解析式
轴截距为6,求此函数解析式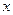 个月内,对某种商品的需求总量
个月内,对某种商品的需求总量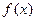 (万件)与月份
(万件)与月份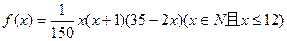 .
.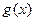 (万件)与月份
(万件)与月份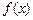 与产量
与产量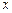 之间的关系式为
之间的关系式为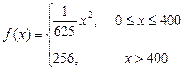 ,每件产品的售价
,每件产品的售价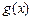 与产量
与产量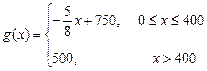 .
.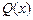 与产量
与产量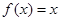 与
与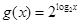 是同一函数.
是同一函数.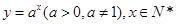 的图像是一些孤立的点.
的图像是一些孤立的点.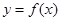 是定义在R上的函数,且
是定义在R上的函数,且 ,则函数
,则函数 轴对称.
轴对称.



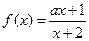 (a为常数)在(-2,2)内为增函数,则实数a的取值范围是
(a为常数)在(-2,2)内为增函数,则实数a的取值范围是 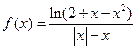 的定义域为
的定义域为 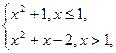 则
则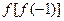 的值为______
的值为______