题目内容
 如图,已知中心在原点0、焦点在x轴上的椭圆T过点M(2,1),离心率为
如图,已知中心在原点0、焦点在x轴上的椭圆T过点M(2,1),离心率为
| ||
| 2 |
(Ⅰ)当直线l0经过椭圆T的左焦点且平行于OM时,求直线l0的方程;(Ⅱ)若斜率为-
| 1 |
| 4 |
分析:(Ⅰ)由椭圆的离心率得到长半轴和短半轴之间的关系,设出椭圆的方程,代入M点的坐标,求出椭圆方程后得到半焦距,求出OM的斜率,则直线l0的方程可求;
(Ⅱ)由题意设出抛物线方程,代入点M的坐标求出抛物线方程,再设出A,B的坐标,由两点式写出AB的斜率,结合斜率为-
求出A,B的纵坐标的和,再由MA和MB的斜率和等于0证出直线MA,MB与X轴总围成等腰三角形.
(Ⅱ)由题意设出抛物线方程,代入点M的坐标求出抛物线方程,再设出A,B的坐标,由两点式写出AB的斜率,结合斜率为-
| 1 |
| 4 |
解答:(Ⅰ)解:由e=
=
,得
=
,
=
,∴a2=4b2.
设椭圆T的方程为
+
=1.
将点M(2,1)代入椭圆方程得:
+
=1,解得b2=2.
∴a2=8.
∴椭圆T的方程为
+
=1.
则c=
=
=
.
因此左焦点为(-
,0),kl0=kOM=
.
∴直线l0的方程为y=
(x+
),
即y=
x+
;
(Ⅱ)证明:如图,
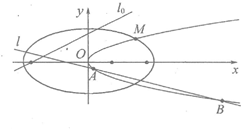
设抛物线方程为y2=2px(p>0),
代入M的坐标得:1=4p,解得:p=
.
∴抛物线C的方程为:y2=
x.
设A(x1,y1),B(x2,y2),直线MA,MB的斜率分别为k1,k2,
则k1=
,k2=
.
kAB=
=
=-
,∴y1+y2=-2.
k1+k2=
+
=
+
=
=0.
∴直线MA,MB与X轴总围成等腰三角形.
| c |
| a |
| ||
| 2 |
| c2 |
| a2 |
| 3 |
| 4 |
| a2-b2 |
| a2 |
| 3 |
| 4 |
设椭圆T的方程为
| x2 |
| 4b2 |
| y2 |
| b2 |
将点M(2,1)代入椭圆方程得:
| 4 |
| 4b2 |
| 1 |
| b2 |
∴a2=8.
∴椭圆T的方程为
| x2 |
| 8 |
| y2 |
| 2 |
则c=
| a2-b2 |
| 8-2 |
| 6 |
因此左焦点为(-
| 6 |
| 1 |
| 2 |
∴直线l0的方程为y=
| 1 |
| 2 |
| 6 |
即y=
| 1 |
| 2 |
| ||
| 2 |
(Ⅱ)证明:如图,

设抛物线方程为y2=2px(p>0),
代入M的坐标得:1=4p,解得:p=
| 1 |
| 4 |
∴抛物线C的方程为:y2=
| 1 |
| 2 |
设A(x1,y1),B(x2,y2),直线MA,MB的斜率分别为k1,k2,
则k1=
| y1-1 |
| x1-2 |
| y2-1 |
| x2-2 |
kAB=
| y2-y1 |
| x2-x1 |
| 1 |
| 2(y1+y2) |
| 1 |
| 4 |
k1+k2=
| y1-1 |
| x1-2 |
| y2-1 |
| x2-2 |
| 1 |
| 2(y1+1) |
| 1 |
| 2(y2+1) |
| y1+y2+2 |
| 2(y1+1)(y2+1) |
∴直线MA,MB与X轴总围成等腰三角形.
点评:本题考查了直线方程的求法,考查了直线与圆锥曲线的位置关系,考查了数学转化思想方法,解答的关键是把要证明的问题转化为两直线的斜率和等于0,是高考试卷中的压轴题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
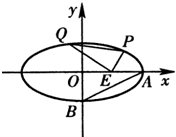 如图,已知中心在原点O、焦点在x轴上的椭圆C的离心率为
如图,已知中心在原点O、焦点在x轴上的椭圆C的离心率为 如图,已知中心在原点且焦点在x轴上的椭圆E经过点A(3,1),离心率
如图,已知中心在原点且焦点在x轴上的椭圆E经过点A(3,1),离心率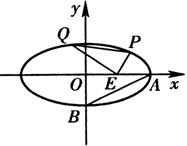
 ,
, ),且它的左焦点F1将长轴分成2∶1,F2是椭圆的右焦点.
),且它的左焦点F1将长轴分成2∶1,F2是椭圆的右焦点.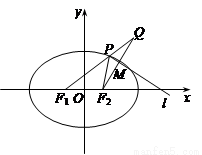 (1)求椭圆的标准方程;
(1)求椭圆的标准方程;