题目内容
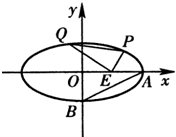
 如图,已知中心在原点且焦点在x轴上的椭圆E经过点A(3,1),离心率e=
如图,已知中心在原点且焦点在x轴上的椭圆E经过点A(3,1),离心率e=
| ||
| 3 |
(1)求椭圆E的方程;
(2)过点A且斜率为1的直线交椭圆E于A、C两点,过原点O与AC垂直的直线交椭圆E于B、D两点,求证A、B、C、D四点在同一个圆上.
分析:(1)设出椭圆的方程,利用椭圆E经过点A(3,1),离心率e=
,可求椭圆的几何量,从而可得椭圆E的方程;
(2)确定B,C,D的坐标,求出过这三点的圆,验证A满足方程即可.
| ||
| 3 |
(2)确定B,C,D的坐标,求出过这三点的圆,验证A满足方程即可.
解答:(1)解:设椭圆方程为
+
=1(a>b>0),因为离心率e=
,所以a2=3b2,…(2分)
所以椭圆方程为
+
=1,
又因为经过点A(3,1),则
+
=1,…(4分)
所以b2=4,所以a2=12,属于椭圆的方程为
+
=1.…(6分)
(2)证明:直线AC的方程为y=x-2,与椭圆方程联立,可得x2-3x=0,∴x=0或x=3,∴C(0,-2)
直线BD的方程为y=-x,与椭圆方程联立,可得x2=3,∴x=±
,∴B(
,-
),D(-
,
)
设经过B,C,D三点的圆的方程为x2+y2+Dx+Ey+F=0,则有
∴D=-1,E=-1,F=-6,∴圆的方程为x2+y2-x-y-6=0,
∵点A(3,1)也适合,∴A(3,1)在圆上,
∴A、B、C、D四点在同一个圆上.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
所以椭圆方程为
| x2 |
| 3b2 |
| y2 |
| b2 |
又因为经过点A(3,1),则
| 9 |
| 3b2 |
| 1 |
| b2 |
所以b2=4,所以a2=12,属于椭圆的方程为
| x2 |
| 12 |
| y2 |
| 4 |
(2)证明:直线AC的方程为y=x-2,与椭圆方程联立,可得x2-3x=0,∴x=0或x=3,∴C(0,-2)
直线BD的方程为y=-x,与椭圆方程联立,可得x2=3,∴x=±
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
设经过B,C,D三点的圆的方程为x2+y2+Dx+Ey+F=0,则有
|
∴D=-1,E=-1,F=-6,∴圆的方程为x2+y2-x-y-6=0,
∵点A(3,1)也适合,∴A(3,1)在圆上,
∴A、B、C、D四点在同一个圆上.
点评:本题考查椭圆的标准方程,考查圆的方程,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 如图,已知中心在原点O、焦点在x轴上的椭圆C的离心率为
如图,已知中心在原点O、焦点在x轴上的椭圆C的离心率为 如图,已知中心在原点0、焦点在x轴上的椭圆T过点M(2,1),离心率为
如图,已知中心在原点0、焦点在x轴上的椭圆T过点M(2,1),离心率为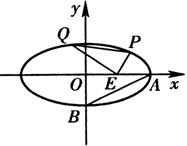
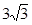 ,
,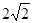 ),且它的左焦点F1将长轴分成2∶1,F2是椭圆的右焦点.
),且它的左焦点F1将长轴分成2∶1,F2是椭圆的右焦点. (1)求椭圆的标准方程;
(1)求椭圆的标准方程;