Question

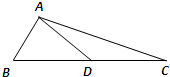（2011•盐城模拟）如图，在△ABC中，BC边上的中线AD长为3，且cosB=

10

8

，cos∠ADC=-

1

4

．
（Ⅰ）求sin∠BAD的值；
（Ⅱ）求AC边的长．

Answer 1

分析：（Ⅰ）根据cosB=

10

8

，cos∠ADC=-

1

4

，利用平方关系，可得sinB、sin∠ADC的值，利用sin∠BAD=sin（∠ADC-∠B），即可求得结论；
（Ⅱ）在△ABD中，由正弦定理，求BD=2，故DC=2，在△ADC中，由余弦定理，可求AC的长．

解答：解：（Ⅰ）因为cosB=

10

8

，所以sinB=

3 6

8

…（2分）
又cos∠ADC=-

1

4

，所以sin∠ADC=

15

4

…（4分）
所以sin∠BAD=sin（∠ADC-∠B）=

15

4

×

10

8

-（-

1

4

）×

3 6

8

=

6

4

…（7分）
（Ⅱ）在△ABD中，由正弦定理，得

3

3 6 8

=

BD

6 4

，解得BD=2…（10分）
故DC=2，从而在△ADC中，由余弦定理，得AC²=9+4-2×3×2×(-

1

4

)=16，所以AC=4…（14分）

点评：本题考查差角的正弦公式，考查正弦定理、余弦定理的运用，属于中档题．