题目内容

精英家教网如图，在等腰梯形ABCD中，M，N分别是AB，CD的中点，沿MN将MNCB折起至MNC1B1，使它与MNDA成直二面角．已知AB=2CD=4MN，给出下列四个等式：
(1)
AN
•
C1N
=0；(2)
B1C1
•
AN
=0；(3)
B1C1
•
AC1
=0；(4)
B1C1
•
AM
=0．中成立的个数是（　　）
A、1B、2C、3D、4
分析：由图形，根据题设中的条件对四个命题逐一判断，即可得出正确答案
解答：解：易知
C1N⊥平面AMN
D，故（1）式成立；同理（4）式也成立；
假设（2）成立，即有
B1C1
⊥
AN
，
．
又由（1）式可得，AN⊥平面B1MNC1，这与AM⊥平面平面B1MNC1矛盾，则（2）式不成立，
对于（3），连接MC1，由B1M=2C1N=4MN，得MC1⊥
B1C1
．
又
B1C1
⊥
AM
，
．
得出
B1C1
⊥
．
平面 A MC1故
B1C1
⊥
．
AC 1
，（3）成立，
故选C
点评：本题考查向量的数量积判断向量的共线与垂直，是向量在立体几何中的重要运用方式，求解本题要注意数形结合，灵活选用判定方法，以达到简化解题的目的．
练习册系列答案
相关题目
精英家教网如图，在等腰梯形ABCD中，AB∥DC，AB=4，CD=2，等腰梯形的高为3，O为AB中点，PO⊥平面ABCD，垂足为O，PO=2，EA∥PO．
（1）求证：BD⊥平面EAC；
（2）求二面角E-AC-P的平面角的余弦值．
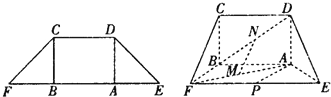如图，在等腰梯形CDEF中，CB、DA是梯形的高，AE=BF=2，AB=2
2
，现将梯形沿CB、DA折起，使EF∥AB，且EF=2AB，得一简单组合体ABCDEF如图所示，已知M、N、P分别为AF，BD，EF的中点．
（1）求证：MN∥平面BCF；
（2）求证：AP⊥平面DAE．
选修4-1；几何证明选讲．
如图，在等腰梯形ABCD中，AD∥BC，AB=DC，过点D作AC的平行线DE，交BA的延长线于点E．
求证：DE•DC=AE•BD．
（2012•河北模拟）如图，在等腰梯形ABCD中，CD=2，AB=4，AD=BC=
2
，E、F分别为CD、AB中点，沿EF将梯形AFED折起，使得∠AFB=60°，点G为FB的中点．
（1）求证：AG⊥平面BCEF
（2）求DG的长度．
如图，在等腰梯形ABCD中，上底CD=3，下底AB=4，E、F分别为AB、CD中点，分别沿DE、CE把△ADE与△BCE折起，使A、B重合于点P．

（1）求证：PE⊥CD；
（2）若点P在面CDE的射影恰好是点F，求EF的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网